Nom donné par S. Collins à une configuration plane composée de triangles rectangles isocèles congruents juxtaposés côté à côté. La juxtaposition peut se faire par un des côtés de l'angle droit ou par l'hypoténuse. Les polyabolos et les polyocèles ont les mêmes triangles unitaires. Toutefois, l'assemblage des triangles pour les polyocèles doit se faire d'une façon déterminée. Deux configurations sont comptées pour une seule si elles coïncident après rotation ou symétrie de l'une d'elles. L'ordre d'un polyabolo correspond au nombre de triangles assemblés. On ne connaît pas de formule générale donnant le nombre de polyabolos d'un ordre donné. Le tableau ci-dessous indique, pour chaque ordre, l'appellation donnée et le nombre de polyabolos différents.

Une fois assemblés, les polyabolos forment des polygones dont le nombre de côtés peut varier. Dans l’illustration suivante, les trois diabolos présentent trois et quatre côtés ; les quatre triabolos présentent quatre et cinq côtés.

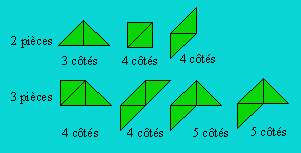
Les polyabolos appartiennent à la classe des polyoïdes. 

© Charles-É. Jean

Index : P