|
Rangée
Dans un treillis, ensemble d’objets
disposés en ligne droite ou selon une certaine symétrie.
Rangée magique
Rangée d’éléments dont la somme est égale à la densité
d’un carré magique. Ces rangées peuvent être linéaires ou brisées.
Rangée linéaire
Dans un carré d’ordre n, une rangée linéaire est formée de n
éléments disposés sur une même ligne, dans une même colonne ou dans une
même diagonale principale. Dans un carré 3 × 3, on peut compter huit
rangées d’éléments : trois rangées horizontales, trois verticales et
deux diagonales. Dans un carré 4 × 4, on peut compter 10 rangées :
quatre horizontales, quatre verticales et deux diagonales. Dans un carré n
× n, on peut compter 2(n + 1) rangées : n
horizontales, n verticales et deux rangées diagonales.
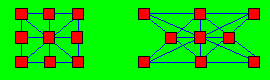
Dans la figure de
gauche ci-après, les neuf petits carrés forment huit rangées. À droite, les
mêmes carrés sont disposés de façon à former 10 rangées.
Rangée brisée
Dans un carré d’ordre n, une rangée brisée est formée de n
éléments qui peuvent être considérés comme des sommets d’une figure
géométrique. Par exemple, les premier et quatrième éléments d’une ligne
combinés avec les deuxième et troisième éléments d’une autre ligne
peuvent constituer une rangée. Outre les 10 rangées linéaires, ce carré
magique comprend 43 rangées dont la somme des éléments est égale à la
densité du carré, soit 34.
|
1 |
8 |
11 |
14 |
|
15 |
10 |
5 |
4 |
|
6 |
3 |
16 |
9 |
|
12 |
13 |
2 |
7 |
Voici
la répartition des rangées :
neuf carrés 2 × 2 : neuf rangées
coins du carré : une rangée
sommets d’un rectangle dont les côtés sont parallèles aux diagonales (A) :
deux rangées
sommets d’un triangle (B) : quatre rangées
sommets de cinq carrés (C) : cinq rangées
sommets de six rectangles (D) : six rangées
sommets de huit parallélogrammes (E) : huit rangées
sommets de huit trapèzes (F) : huit rangées

Index
: R
© Charles-É. Jean
|
![]()
![]()