|
Renversée
° Pyramide renversée.
– Récréation d'origine inconnue concernant la représentation d'un nombre
triangulaire : Six boules sont placées sous une forme triangulaire
régulière. Combien de boules au minimum doit-on déplacer pour obtenir une
configuration identique ?
Le problème peut être généralisé avec des
boules dont le nombre correspond à un nombre triangulaire de rang n où n
est le nombre de boules à la base de la pyramide. Le tableau suivant indique le
nombre m de boules à déplacer en fonction de n boules à la base.
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
m |
0 |
1 |
2 |
3 |
5 |
7 |
9 |
12 |
15 |
18 |
Pour trouver le nombre minimal de boules, on divise par 3 le
nombre total de boules de la pyramide et on conserve la partie entière du
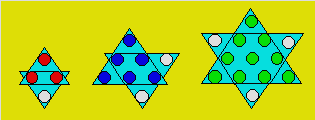
quotient. Dans les figures suivantes, les boules blanches sont celles qui ont
été déplacées de l'extérieur à l'intérieur du triangle lorsque la base
contient respectivement 2, 3 et 4 boules.
Ce problème appartient à la classe des récréations de construction.
© Charles-É. Jean
Index
: R
|
![]()
![]()