Au pays des Lumettes, les arbres ressemblent à des allumettes.  L’Allumeur en chef a aménagé un parc. Dix-huit arbres sont disposés à trois mètres l’un de l’autre en lignes et en colonnes.

Lumine se rend au pied de l’arbre bleu dans le coin supérieur gauche. Elle se dirige vers la droite en saluant au passage chaque arbre. Soudain, elle s’arrête. Elle repart dans le même sens et parcourt 47 mètres toujours en saluant chaque arbre au passage. Elle fait un retour de 27 mètres, puis avance à nouveau de 11 mètres. Elle atteint alors l’arbre de départ.

Au début de sa course,  quelle a été la distance minimale parcourue par Lumine avant de s’arrêter ?

Solution

Dans un catalogue de jeux, Anémone a vu le cube ci-après. Elle s’est procuré des petits cubes de même grandeur ; puis elle les a assemblés en laissant vide l’intérieur du grand cube. Toutefois, afin de jouer un tour à son ami, avant de fermer la dernière face, elle a mis des morceaux de chocolat noir à l’intérieur.

On ne connaît pas la quantité de chocolat déposée par Anémone ; mais on peut trouver le nombre de cubes qui ont été nécessaires pour établir cette structure cubique. 

Quel est ce nombre ?

Solution

71. Un carré

Prenez un A, un C, un D, un F et un H. 

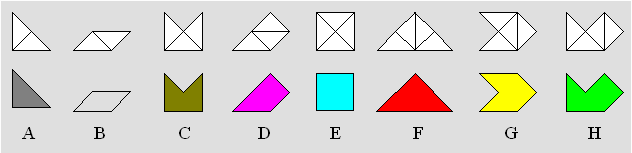
Construisez un carré.

Solution

© Charles-É. Jean