Dictionnaire de mathématiques récréatives Cube magique

Magique

° Cube magique. – 1^e Arrangement de n³ nombres disposés en forme de cube de telle manière que chacune des n lignes et des n colonnes de chacun des n plans, chacun des n² piliers, et chacune des quatre triagonales principales ont la même somme.

Le cube magique normal d'ordre 3 est constitué des 27 entiers de 1 à 27 ; sa densité est 42. Cette somme apparaît dans 31 rangées : 27 rangées parallèles aux arêtes et les quatre triagonales.

Voici un cube magique d'ordre 3 constitué des entiers de 1 à 27 présenté en trois plans, lesquels doivent être placés l'un sur l'autre :

6	16	20	26	3	13	10	23	9
17	21	4	1	14	27	24	7	11
19	5	18	15	25	2	8	12	22

La densité d'un cube magique d'ordre n composé des entiers consécutifs de 1 à n³ est n(n³ + 1)/2. Les procédés de construction des cubes magiques s'inspirent de ceux utilisés pour les carrés magiques.

Des travaux sur le sujet ont permis de définir des types variés de cubes magiques de différents ordres. A. Adler et R. Shuo-yen ont montré en 1977 un procédé pour transformer un cube magique d’ordre n en carrés magiques d’ordre 2n.

Les quatre premiers carrés sont les quatre piliers d’un cube magique. On a d'abord le pilier supérieur, le 2 le 3 et l'inférieur.

1	63	62	4	48	18	19	45	32	34	35	29	49	15	14	52
60	6	7	57	21	43	42	24	37	27	26	40	12	54	55	9
56	10	11	53	25	39	38	28	41	23	22	44	8	58	59	5
13	51	50	16	36	30	31	33	20	46	47	17	61	3	2	64

Ces trois carrés d’ordre 8 sont magiques. Le premier provient de la suite des termes horizontalement, le deuxième verticalement et le troisième par pilier.

1	63	62	4	60	6	7	57	1	62	48	19	32	35	49	14	1	48	32	49	63	18	34	15
56	10	11	53	13	51	50	16	60	7	21	42	37	26	12	55	62	19	35	14	4	45	29	52
48	18	19	45	21	43	42	24	56	11	25	38	41	22	8	59	60	21	37	12	6	43	27	54
25	39	38	28	36	30	31	33	13	50	36	31	20	47	61	2	7	42	26	55	57	24	40	9
32	34	35	29	37	27	26	40	63	4	18	45	34	29	15	52	56	25	41	8	10	39	23	58
41	23	22	44	20	46	47	17	6	57	43	24	27	40	54	9	11	38	22	59	53	28	44	5
49	15	14	52	12	54	55	9	10	53	39	28	23	44	58	5	13	36	20	61	51	30	46	3
8	58	59	5	61	3	2	64	51	16	30	33	46	17	3	64	50	31	47	2	16	33	17	64

Le cube magique peut être géométrique, pantriagonal, parfait ou premier.

2^e Un cube est magique sur ses faces lorsque la somme des nombres disposés sur les arêtes qui délimitent chaque face est la même pour chaque face. Le cube ayant 12 arêtes, on doit y placer 12 nombres. Il est possible de réaliser un cube magique avec les entiers de 1 à 12. La densité est alors 26. Il existe 80 solutions différentes. En voici une :

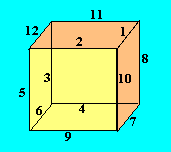
Le cube, étant le dual de l'octaèdre, les deux figures ont les mêmes solutions. De plus, l'hexagramme a les mêmes solutions.

3^e Un cube est magique sur ses sommets lorsque la somme des nombres disposés sur les trois arêtes qui se rencontrent en un sommet est la même pour chaque sommet. Le cube ayant 12 arêtes, on doit y placer 12 nombres. Il n'existe pas de cube magique formé des entiers de 1 à 12.

Voici un cube magique dont la somme pour chaque sommet est 22 :

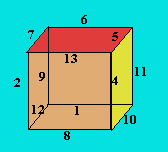
Le cube magique appartient à la classe des treillis magiques.

Index : M