Récréations magiques

Série A

53. Tasses de Débora

Débora marque par des numéros ses neuf tasses de collection de la façon suivante :

Elle veut les disposer en un carré 3 × 3. Le résultat dans chacune des huit rangées doit être le même. Ce résultat provient de la somme des deux éléments extrêmes de chaque rangée à laquelle on soustrait le nombre du milieu de cette rangée. Par exemple, dans une rangée, si on a 2, 3 et 6 dans cet ordre, le résultat est 2 - 3 + 6 = 5.

Formez un carré en agençant les neuf tasses.

Solution

L’Anthologie grecque contient de nombreuses récréations dont quatre d’héritage.

Série B

53. Normand calcule

Normand découpe neuf jetons et inscrit les numéros de 2 à 14, sauf 8, 9, 10 et 13.

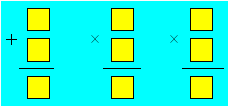
Placez les jetons sur les cases vides de façon à réaliser les trois opérations.

Solution

À l’aide d’opérations simples, représentez 6 avec deux 2 et deux 6.

Solution

Série C

53. Un N entremêlé

Dans les cellules, disposez chaque nombre de 1 à 7. La somme doit être 10 dans chacune des six rangées de deux ou de trois cellules reliées par une droite.

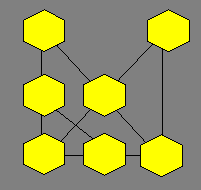
Le code de ce treillis peut être 7 - 6 - (2, 3) - 250 - 02.

Solution

À tous les trois ans, pour un même quantième et un même mois, le jour de la semaine recule de trois rangs s’il y a un 29 février dans l’intervalle.