Récréations magiques

Série A

95. Jeu de Coralie

Coralie est en train de composer un jeu de société. À tour de rôle, chaque joueur doit déposer un jeton sur un tableau comportant six cases disposées comme ci-dessous. Le matériel consiste en 11 jetons numérotés de 3 à 13. Pendant la partie, chaque joueur a droit de consulter les configurations possibles de jetons.

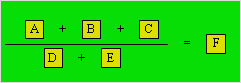
Coralie veut connaître le nombre de configurations qui respectent les conditions suivantes :

1. A est plus petit que B et B est plus petit que C.

2. D est plus petit que E.

3. D = 4 et F = 3.

4. Le jeton 6 n’est pas utilisé.

Combien y a-t-il de configurations possibles ?

Solution

La tour est une pièce du jeu d'échecs qui se déplace sur une case quelconque parallèlement aux côtés de l'échiquier, franchissant autant de cases vides qu'il convient.

Série B

95. Élèves de Jocelyn

Huit élèves de Jocelyn portent un gilet numéroté. Les enfants se placent comme ci-après.

1. La somme des numéros est 20 dans chaque rangée de trois enfants.

2. Le numéro 6 est voisin et à gauche du 10.

3. Le 4 est dans le coin opposé du 3, le 3 étant en haut à droite du 4.

4. Le numéro E est le double du A.

Comment sont placés les enfants ?

Solution

Un trait réalisé sans que le crayon soit levé est dit continu.

Série C

95. Une double somme

Dans les cellules, disposez chaque nombre de 1 à 10 pour que la somme soit 22 sur chaque ligne et 11 dans chaque colonne.

Le code de ce treillis peut être 10 - 4 - (3, 4) - 46 - 02.

Solution

Je choisis un nombre inférieur à 300 et ayant trois chiffres différents. J’additionne 78. J’obtiens un nombre qui contient un 1, un 3 et un 9. Quel est le nombre choisi ?

Solution