Série A

Solution 16

La somme des nombres de 1 à 11 est 66. La première rangée verticale, la première horizontale et la troisième horizontale totalisent 3 ´ 17 = 51. On fait 66 - 51 = 15. Il reste 15 pour la tuile centrale et celle à sa gauche. Elles valent 11 et 4 dans cet ordre. La tuile de gauche vaut 2. En excluant 11, les combinaisons possibles de trois nombres dont la somme est 17 sont : (1, 6, 10), (1, 7, 9), (2, 5, 10), (2, 6, 9), (2, 7, 8), (3, 4, 10), (3, 5, 9), (3, 6, 8), (4, 5, 8) et (4, 6, 7). On vérifie les combinaisons dans la première rangée verticale. Seuls 5 et 10 y sont possibles. On fait de même pour les deux autres rangées. Voici une disposition :

Retour au problème

Les propositions mathématiques sont reçues comme vraies parce que personne n’a intérêt qu’elles soient fausses. 

Montesquieu (1689-1755)

Série B

Solution 16

La somme des deux nombres placés est 20 ; celle des nombres à placer est 34. La somme totale est 54. Comme il y a trois lignes (ou trois colonnes), la somme doit être 54/3 = 18 sur chaque ligne (ou dans chaque colonne). Le nombre du milieu est 6, car il est le tiers de la somme de chaque rangée. On complète par calculs. La distribution est :

Retour au problème

En topologie, un beigne est un objet qui a un seul trou. À la suite de distorsions, un beigne peut être transformé en une tasse, conservant son unique trou.

Série C

Solution 16

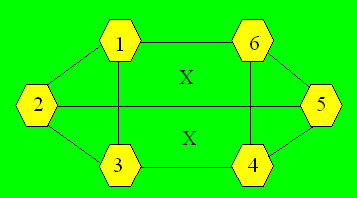
Les combinaisons de deux nombres dont la somme est la moitié de 14 sont : (1, 6), (2, 5) et (3, 4). On place ces trois couples horizontalement. Une configuration est :

Retour au problème

Solution de l'énigme
Le premier nombre est CENT ; le deuxième est CINQ ; le troisième est CINQUANTE.