Série A

Solution 22

Les triplets dont la somme est 8 sont : (1, 2, 5), (1, 3, 4).
Les triplets dont la somme est 9 sont : (1, 3, 5), (2, 3, 4).
Les triplets dont la somme est 10 sont : (1, 2, 7), (1, 4, 5), (2, 3, 5).
Les triplets dont la somme est 11 sont : (1, 3, 7), (2, 4, 5).

Chaque nombre du centre de chaque côté du triangle doit apparaître trois fois dans les combinaisons précédentes. On commence par placer ces nombres en tenant compte des trois sommes voisines. La configuration est :

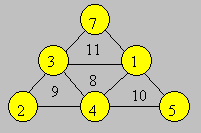
Retour au problème

Série B

Solution 22

On commence par les martiens et on compte les groupes où une personne peut parler aux autres qui suivent. M1 peut parler à J2, J4, J6, L4, L6, L8 (six groupes). M3 peut parler aux mêmes personnes (six groupes). M2 peut parler à J3, J5, L3, L5, L7 (cinq groupes). M4 peut parler aux mêmes personnes (cinq groupes). J2 peut parler à L3, L5, L7 (trois groupes). J4 peut parler aux mêmes personnes (trois groupes) ; J6 aussi (trois groupes). J3 peut parler à L4, L6, L8 (trois groupes). J5 peut parler aux mêmes personnes (trois groupes). 

En tout, 37 groupes de personnes pourront se parler.

Retour au problème

Solution 22

Les combinaisons de trois nombres dont la somme est 12 sont : (1, 4, 7), (1, 5, 6), (2, 3, 7), (2, 4, 6), (3, 4, 5). Une configuration est :

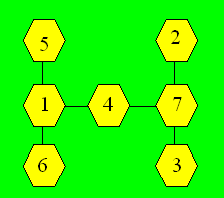
Retour au problème