Série A

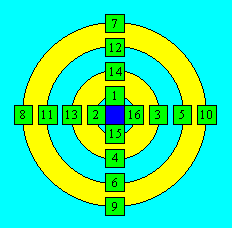
Solution 27

Dans la suite des nombres de 1 à 16, la somme des deux nombres également distants du centre est 17. Les combinaisons sont : (1, 16), (2, 15), (3, 14), (4, 13), (5, 12), (6, 11), (7, 10) et (8, 9). On prend deux combinaisons. Par exemple, on place successivement (1, 2, 15, 16), ( 3, 4, 13, 14), (5, 6, 11, 12) et (7, 8, 9, 10) dans les quatre couronnes. En même temps, on dispose les nombres pour avoir une somme de 15 et une autre de 19 dans chaque rangée. Voici une configuration :

Retour au problème

Solution de l’énigme 
Il existe 7 multiples.

Série B

Solution 27

Le 5 doit apparaître dans la rangée du 16 ou du 18. Il ne peut pas être dans le coin, car il serait dans les deux rangées. Il y a deux possibilités : sous le 3 ou à droite du 4. Après des essais, on le place sous le 3. On complète la dernière rangée horizontale avec 6 et 8 dans cet ordre. Il reste à placer 7, 9 et 10. La disposition est :

Retour au problème

Dans son livre Triparty en la science des nombres, Nicolas Chuquet (1445-1500) a posé des récréations comme celle des d.

Série C

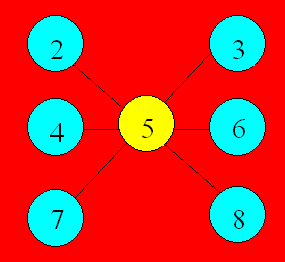
Solution 27

La somme des nombres de 2 à 8 est 35. Trois rangées de 15 totalisent 45. On fait 45 - 35 = 10 et 10 ¸ 2 = 5. Le nombre du centre doit être 5. Une configuration est :

Retour au problème

On peut parier 12 255 contre 307, ou près de 40 contre 1, qu'un enfant de six ans vivra un an de plus.

Citation de Buff