Série A

Solution 47

La somme des trois sommes horizontales est 12 + 14 = 26. Ce sont 7, 9 et 10. On a 2 + 5 = 7 car le 1 et le 7 ne sont pas sur la même ligne. On a 1 + 8 = 9, puis 4 + 6 = 10. Comme le 6 et le 8 ne sont pas dans la même colonne, on a : 1 + 5 + 6 = 12 et 2 + 4 + 8 = 14. Voici le tableau complété :

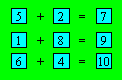
Retour au problème

Les nombres sont pour nous de vieilles connaissances. Nous avons grandi en leur compagnie et nous les rencontrons tous les jours.

Série B

Solution 47

Comme le premier nombre est supérieur de 9 au deuxième, les unités possibles des deux premiers nombres sont (2, 3), (3, 4), (4, 5) ou (5, 6). Comme le troisième nombre est supérieur de 15 au deuxième, les unités possibles des deux derniers nombres sont (1, 6) ou (6, 1). D’où, dans l’ordre, les unités sont (5, 6, 1). On complète les dizaines. 

La disposition est : 35 + 26 - 41 = 20.

Retour au problème

Solution de l’énigme 
Il n’y a rien. Le milieu de TOUT est entre TO et UT.

Série C

Solution 47

Les combinaisons de trois nombres dont la somme est 12 sont : (1, 4, 7), (1, 5, 6), (2, 3, 7), (2, 4, 6), (3, 4, 5). Seul le 4 se trouve dans trois combinaisons. On le place dans la cellule centrale. Une configuration est :

Retour au problème