|
Série A
Solution 56
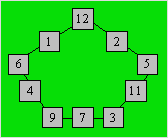
Les nombres dans les cellules colorées sont : (1, 12), (2, 11), (4, 9),
(6, 7). Les deux blanches vont recevoir 3 et 5. Première
hypothèse : On place 3 en haut et 5 plus bas. Le centre est alors 11. L’autre
cellule grise reçoit 13 - 11 = 2. On devrait compléter la rangée du 2 avec
14 : ce qui est impossible. Deuxième hypothèse : On place le 5 en
haut et le 3 plus bas. Alors, le centre est 11. L’autre cellule grise reçoit
13 - 11 = 2. On complète la rangée avec 12. L’autre cellule jaune reçoit 1.
On complète avec 6. L’autre cellule bleue reçoit 13 - 6 = 7. On complète la
rangée avec 9, puis l’autre avec 4. Voici la disposition des nombres :
Retour
au problème
|
Dans
la résolution d’un problème, la démarche est laborieuse si
l’élève a adopté une stratégie qui exige un trop grand nombre
d’opérations et de calculs.
|
|
Série B
Solution 56
On complète la première ligne avec C et D dans cet ordre, car D est dans la
troisième colonne. On complète la première colonne avec D et A, car D est sur
la quatrième ligne. On complète la première diagonale avec A et C. On
complète la quatrième ligne avec E et B. On continue ainsi. La grille remplie
est :
|
E |
B |
C |
D |
A |
|
D |
A |
E |
B |
C |
|
B |
C |
D |
A |
E |
|
A |
E |
B |
C |
D |
|
C |
D |
A |
E |
B |
Retour
au problème
|
Solution
de l’énigme
ÉLÉPHANT
|
|
Série C
Solution 56
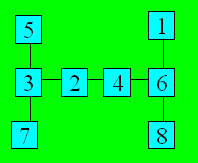
Les combinaisons de trois nombres dont
la somme est 15 sont : (1, 6, 8), (2, 5, 8), (2, 6, 7), (3, 4, 8), (3, 5,
7), (4, 5, 6). Une configuration est :
Retour
au problème
|
Quand
on relie deux points quelconques situés à l’intérieur d’un polygone
concave, certains points de la droite peuvent être à l’extérieur du
polygone. |
![]()
![]()