|
Polygone
Figure
géométrique plane limitée par des
segments. Ces segments sont les côtés du
polygone. Un polygone peut être divisé en autant de triangles
qu’il a de côtés moins deux. Par exemple, un pentagone
peut être partagé en trois triangles.
Côtés congrus
Côtés qui ont la même longueur. Dans un
triangle équilatéral,
les trois côtés sont congrus. Dans un triangle rectangle isocèle,
les deux côtés autres que l’hypoténuse sont congrus.
Sommet
Point de
rencontre de deux segments dans un polygone. Deux sommets qui se suivent sont
dits consécutifs.
Diagonale
Segment de droite qui relie deux
sommets non consécutifs dans un polygone. Voici un tableau qui donne le nombre
de diagonales d dans un polygone à n côtés ou sommets lorsque n
varie de 3 à 10 :
|
n |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
d |
0 |
2 |
5 |
9 |
14 |
20 |
27 |
35 |
44 |
54 |
Un carré
a deux diagonales ; un pentagone en a
cinq ; un hexagone en a neuf.
Pour
trouver le nombre de diagonales dans un polygone de n côtés où n
est plus grand ou égal à 3, on peut raisonner ainsi : À partir d’un
sommet, on peut tracer (n - 3) diagonales. On exclut ainsi le sommet de
départ et ses deux sommets consécutifs, tous trois ne pouvant pas être l’aboutissement
d’une diagonale.
Par exemple, à partir d’un sommet d’un décagone,
on peut tracer 10 - 3 = 7 diagonales. Comme il y a 10 sommets, on fait 10 ´
7 = 70. Comme chaque diagonale est comptée deux fois, on divise par 2. On fait
70 ¸ 2 = 35. Un décagone a 35 diagonales.
On
généralise ainsi : Dans un polygone de n côtés, le nombre de
diagonales est égal à n(n - 3)/2. Pour trouver le nombre de
diagonales d’un heptagone,
on fait : 7 ´
4 ¸ 2 = 14.
Connaissant le nombre de diagonales d d’un polygone
à n côtés, le nombre de diagonales d’un polygone ayant un côté de
plus est (n + d - 1). Lorsque le nombre de côtés est impair, on
a successivement 3 ´ 0 = 0, 5
´ 1 = 5, 7 ´
2 = 14, 9 ´ 3
= 27, 11 ´ 4 = 44 diagonales. Lorsque le nombre de
côtés est pair, on a successivement 4 ´
1/2 = 2, 6 ´ 3/2 = 9, 8 ´
5/2 = 20,
10 ´ 7/2 = 35, 12 ´
9/2
= 54 diagonales.
Le nombre de diagonales est un nombre triangulaire diminué de
1.
Les diagonales issues d'un sommet divisent ce polygone en
autant de triangles qu'il a de côtés moins deux.
Angle
intérieur
Angle formé par deux côtés issus du
même sommet. La somme des angles intérieurs de certains polygones est donnée
dans ce tableau.
De façon générale, la somme des angles intérieurs d’un
polygone ayant n côtés est (n - 2)180
degrés.
Angle extérieur
Angle formé par un côté et le
prolongement du côté adjacent. La somme des mesures de l’angle intérieur d’un
polygone et celles de l’angle extérieur adjacent est égale à 180 degrés ou
deux droits.
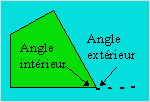
La somme des angles intérieurs et extérieurs d’un
polygone est égale au produit du nombre de côtés par deux droits ou 2n
droits. Comme la somme des angles intérieurs est (n - 2)180º, on
soustrait cette somme de 2n. La somme des angles extérieurs est égale
à quatre droits ou 360º.
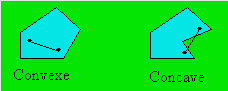
Polygone convexe
Un polygone est convexe lorsqu’il n’y
a pas d’angle rentrant ou de partie rentrante.
Quand on relie deux points quelconques situés à l’intérieur du polygone,
tous les points de la droite sont à l’intérieur du polygone. La mesure de
tout angle intérieur d'un polygone convexe est inférieure à 180 degrés.
Polygone concave
Un polygone est concave quand il y a au
moins un angle rentrant ou une partie rentrante. Quand on relie deux points
quelconques situés à l’intérieur du polygone, certains points de la droite
peuvent être à l’extérieur du polygone. Un polygone concave possède au
moins un angle intérieur dont la mesure est supérieure à 180 degrés.
Appellation des polygones
On nomme un polygone en fonction du
nombre de ses côtés. Les deux
tableaux suivants donnent le nom des polygones dont le
nombre de côtés est égal ou inférieur à 12 :
Au-delà
de 12 côtés, on parle généralement de polygone à n
côtés. Toutefois, pour certains de ces polygones, des appellations existent.
Voici le nom des polygones de 13 à 20 côtés :
|
13 côtés |
14 côtés |
15 côtés |
16 côtés |
|
tridécagone |
tétradécagone |
pentadécagone |
hexadécagone |
|
17 côtés |
18 côtés |
19 côtés |
20 côtés |
|
heptadécagone |
octadécagone |
ennéadécagone |
icosagone |
Polygone régulier
Un polygone est régulier quand ses
côtés sont congrus et que ses angles ont la même mesure. Un polygone
régulier est équilatéral et équiangle. Le tableau suivant donne la mesure de
l’angle extérieur et celle de l’angle intérieur pour certains polygones
réguliers.
|
Polygone régulier |
Mesure de l’angle extérieur |
Mesure de l’angle intérieur |
Somme |
|
Triangle équilatéral |
120° |
60° |
180° |
|
Carré |
90° |
90° |
180° |
|
Pentagone |
72° |
108° |
180° |
|
Hexagone |
60° |
120° |
180° |
|
Heptagone |
51,43° |
128,57° |
180° |
|
Octogone |
45° |
135° |
180° |
|
Décagone |
36° |
144° |
180° |
|
Dodécagone |
30° |
150° |
180° |
Par exemple, l’angle extérieur d’un pentagone régulier
mesure 72°. Son angle intérieur est de 108°. Leur somme est de 180°.
Apothème
d’un polygone régulier
Perpendiculaire abaissée du centre du
polygone sur un côté. L'apothème d'un polygone régulier est égal à la
longueur du côté multipliée par un coefficient déterminé par le nombre de
côtés. Voici le coefficient pour certains polygones réguliers :
|
triangle |
carré |
pentagone |
hexagone |
heptagone |
octogone |
décagone |
dodécagone |
|
0,289 |
0,5 |
0,688 |
0,866 |
1,038 |
1,270 |
1,539 |
1,866 |
Par exemple, l'apothème d'un hexagone régulier est égal à
la longueur du côté multipliée par 0,866. Dans un hexagone de 10 centimètres
de côté, l'apothème est égal à : 10 × 0,866 = 8,66 centimètres.
Aire d’un polygone régulier
L'aire d'un polygone régulier est
égale au produit de son demi-périmètre par la longueur de son apothème. En effet, on peut
décomposer le polygone en n triangles de même grandeur.
L’aire d’un
triangle est le demi-produit de sa base par sa hauteur, soit (b × h)/2.
Le côté du polygone est la base ; l’apothème est la hauteur. Alors, l’aire
du polygone est égale à (nb × h)/2, nb étant la mesure
du périmètre et h la mesure de l’apothème. Le tableau suivant donne
l’aire d’un polygone régulier lorsque le côté du polygone mesure une
unité.
|
triangle |
carré |
pentagone |
hexagone |
heptagone |
octogone |
décagone |
dodécagone |
|
0,433 |
1 |
1,721 |
2,598 |
3,634 |
4,828 |
7,694 |
11,196 |
Soit un hexagone de 10 centimètres de côté, son aire est
égale à : 6 × 10/2 × 8,66 = 259,8 centimètres carrés.
Polygone inscrit
Un
polygone est inscrit dans un cercle quand tous ses sommets sont sur le
cercle.
Polygone circonscrit
Un polygone est circonscrit à un cercle
quand tous ses côtés sont tangents au cercle. Le cercle est alors
inscrit dans le polygone.
Longueur du côté d’un polygone
inscrit dans un cercle
La longueur du côté d’un triangle
équilatéral inscrit dans un cercle de rayon R est égale à R√ 3.
Sa valeur rapprochée est 1,732R.
La longueur du côté d’un
carré inscrit dans un cercle de rayon R est égale à R√2.
Sa valeur rapprochée est 1,414R.
La longueur du côté d’un
hexagone régulier inscrit dans un cercle de rayon R est égale à R.
La longueur du côté d’un
octogone régulier inscrit dans un cercle de rayon R est égale au produit
de R et de la racine carrée de (2 - √2).
Sa valeur rapprochée est 0,765R.
Longueur de l’apothème d’un
polygone inscrit dans un cercle
La longueur de l’apothème d’un
triangle équilatéral inscrit dans un cercle de rayon R est égale à
R/2.
La longueur de l’apothème d’un
carré inscrit dans un cercle de rayon R est égale à R√2/2.
Sa valeur rapprochée est 0,707R.
La longueur de l’apothème d’un
hexagone régulier inscrit dans un cercle de rayon R est égale à R√3/2.
Sa valeur rapprochée est 0,866R.
La longueur de l’apothème d’un
octogone régulier inscrit dans un cercle de rayon R est égale au produit
de R/2 et de la racine carrée de (2 - √2).
Sa valeur rapprochée est 0,382R.
Polygones remarquables
Les polygones remarquables sont :
1er le
triangle, dont le triangle équilatéral, le triangle isocèle, le triangle
rectangle,
2e le
quadrilatère, dont le carré, le rectangle, le losange, le parallélogramme et
le trapèze,
3e le
pentagone régulier,
4e l’hexagone régulier.
© Charles-É. Jean
Index
: P
|
Voir aussi
Polygone dans le Dictionnaire de mathématiques
récréatives.
|
![]()
![]()