|
Série A
Solution 58
La somme des numéros est 42. Les numéros placés aux
extrémités de la rangée horizontale doivent être comptés une seconde fois
à cause de l’intersection des rangées. Les deux plus petits numéros ont une
somme de 7. On fait 42 + 7 = 49 et 49
¸
3 = 16,3.
Pour avoir une somme de 17, il faut placer dans la rangée horizontale deux
numéros dont la somme est 9. Le terme central sera alors 8.
Le poussin 8 devra être placé dans la case centrale.
À titre d’exemple, voici une disposition des poussins :
Retour
au problème
|
Un
triangle
équilatéral
peut avoir un centre qui est l’intersection
des trois bissectrices, mais ce n’est pas un point de symétrie.
|
|
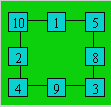
Série B
Solution 58
La première rangée horizontale et la
première rangée verticale doivent être complétés avec (1, 5) et (2, 4).
Avec 9, les combinaisons possibles dont la somme est 16 sont (3, 4) et
(2, 5). Avec 8, la seule combinaison possible est (3, 5). Voici une
disposition :
Retour
au problème
|
Le
mathématicien suisse Leonhard Euler (1707-1783) a résolu de nombreux
problèmes comme celui des officiers.
|
|
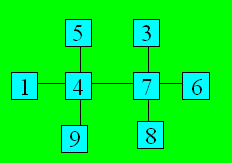
Série C
Solution 58
Les combinaisons de trois nombres dont
la somme est 18 sont : (1, 8, 9), (3, 6, 9), (3, 7, 8), (4, 5, 9), (4, 6,
8), (5, 6, 7). Une configuration est :
Retour
au problème
|
Solution
de l’énigme
Ce nombre est 27.
|
![]()
![]()