Série A

Solution 65

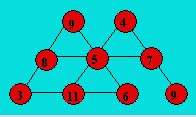
Les combinaisons de trois nombres dont la somme est 20 sont : (3, 6, 11), (3, 8, 9), (4, 5, 11), (4, 7, 9), (5, 6, 9) et (5, 7, 8). Il y a deux combinaisons comportant un 3 : (3, 6, 11) et (3, 8, 9). Comme le 8 doit être immédiatement à gauche du 5, on place le 8 dans la deuxième rangée horizontale à gauche et le 5 au centre. On complète la deuxième rangée oblique avec 9 et 6. Il reste à placer 4, 7 et 11. Voici une disposition des nombres :

Retour au problème

Série B

Solution 65

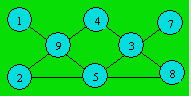
Les combinaisons possibles de trois nombres dont la somme est 15 sont : (1, 5, 9), (2, 4, 9), (2, 5, 8), (3, 4, 8), (3, 5, 7). Le 5 est le seul nombre qui apparaît trois fois. On le place au milieu de la rangée horizontale inférieure. On complète cette rangée avec (2, 8) : c’est la seule combinaison possible car 3 et 9 sont déjà placés. Il reste à placer 1, 4 et 7. Une disposition est :

Retour au problème

Série C

Solution 65

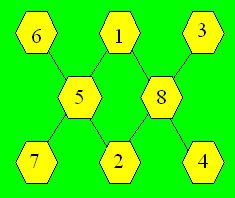
Quatre cellules appartiennent à deux rangées et les quatre autres à une seule rangée. Si on place 1, 2, 3 et 4 dans les cellules de deux rangées et 5, 6, 7 et 8 dans les autres, on peut écrire : 2(1 + 2 + 3 + 4) + (5 + 6 + 7 + 8) = 46. Comme la somme est 13 et qu’il y a quatre rangées, la somme doit être 52 au lieu de 46. On ramène 5 et 8 dans la première partie contre 3 et 4. On a : 2(1 + 2 + 5 + 8) + (3 + 4 + 6 + 7) = 52. Une configuration est :

Retour au problème