Angles complémentaires
Deux angles sont complémentaires
lorsque la somme de leur mesure est égale à 90 degrés ou à un droit (figure
P ci-dessous). Si un angle mesure 42 degrés et un autre 48 degrés, les deux
mesurent 90 degrés ; ils sont complémentaires l’un de l’autre. Le
complément d’un angle est la mesure qu’il faut ajouter à l’un pour
obtenir 90 degrés.
Angles supplémentaires
Deux angles sont supplémentaires
lorsque la somme de leur mesure est égale à 180 degrés ou à deux droits
(figure Q). Si un angle mesure 110 degrés et un autre 70 degrés, les deux
mesurent 180 degrés ; ils sont supplémentaires l’un de l’autre. Le
supplément d’un angle est la mesure qu’il faut ajouter à l’un pour
obtenir 180 degrés.
Angles opposés par le sommet
Deux angles sont opposés par le
sommet, si les côtés de l’un sont les prolongements des côtés de l’autre
(figure R).
Bissectrice d’un angle
Droite qui, passant par un sommet,
partage cet angle en deux angles de même mesure. Dans la figure S, le côté
commun est une bissectrice.
Angles congrus
Deux angles sont congrus lorsqu’ils
ont la même mesure. Exemple. Les deux angles de la figure S sont congrus.
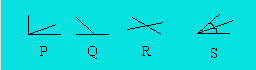
Les angles opposés par le sommet sont congrus.
Angles adjacents
Deux angles sont adjacents quand ils
ont un point commun et qu’ils sont situés de part et d’autre d’un côté
commun. Les angles ADB et BDC ci-après en P sont adjacents. Le côté commun
est DB et le point commun est D.
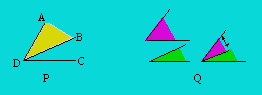
Pour obtenir la somme de deux angles, on les dispose pour qu’ils
forment des angles adjacents. Pour obtenir la différence de deux angles, on
superpose le plus petit angle sur le plus grand. Dans la figure Q, on a d’abord
deux angles. Leur différence est l’angle muni d’une flèche.
Des angles
adjacents qui ont leurs côtés extérieurs en ligne droite sont
supplémentaires. Lorsque deux droites se coupent, la somme des deux angles
adjacents égale deux droits.
© Charles-É. Jean
Index
: A
![]()
![]()