|
Triangle
Polygone
formé de trois côtés et de trois angles. Lorsque
trois droites se coupent deux à deux, elles forment un triangle. On peut
définir le triangle par rapport à la longueur de ses côtés.
Triangle isocèle
Un triangle isocèle a deux côtés
ayant la même longueur. La figure P ci-après montre un triangle isocèle. Les
deux côtés marqués ont la même longueur. Dans tout triangle
isocèle, les angles opposés aux côtés congrus
sont congrus.
Triangle équilatéral
Un triangle équilatéral
a trois
côtés ayant la même longueur. La figure Q ci-après montre un triangle
équilatéral. Les trois côtés ont la même longueur. Les
angles mesurent chacun 60 degrés.
Triangle scalène
Un triangle scalène a trois côtés de
longueur différente. La figure R montre un triangle scalène.
On peut aussi définir le triangle par rapport à la mesure
de ses angles.
Triangle obtusangle
Un triangle obtusangle a un angle obtus. La figure R montre un triangle obtusangle. Un angle mesure plus de 90
degrés.
Triangle acutangle
Un triangle acutangle a trois angles aigus. La figure P montre un triangle acutangle. Chacun des trois angles mesure
moins de 90 degrés.
Triangle équiangle
Autre appellation d’un triangle
équilatéral.
Triangle rectangle
Un triangle rectangle a un angle
droit.
La figure S représente un triangle rectangle.
Triangle rectangle isocèle
Un triangle rectangle isocèle est un
triangle rectangle ayant deux côtés de même longueur. La figure T représente
un triangle rectangle isocèle. Les deux côtés marqués ont la même longueur.
Dans tout triangle rectangle isocèle, chacun des angles aigus
mesure 45 degrés.

Dans un triangle, certaines droites ont reçu une
appellation.
Base
La base est le côté opposé à un
sommet donné. Pour des raisons pratiques, on choisit souvent le côté
inférieur. Dans le triangle P ci-après, AB est la base par rapport à C, BC
est la base par rapport à A, AC est la base par rapport à B.
Hauteur
La hauteur est une perpendiculaire qui
joint un sommet et la base correspondante (ou son prolongement). Dans le
triangle P, EB est une hauteur.
Médiane
La médiane est la droite qui joint un
sommet et le milieu de la base correspondante. Dans le triangle Q, EB est une
médiane.
Médiatrice
La médiatrice est une perpendiculaire
élevée au milieu d’un côté de ce triangle. Dans le triangle Q, FG est une
médiatrice.
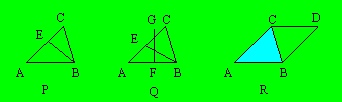
L’aire d’un triangle est égale à la moitié du
parallélogramme qui a la même base et la même hauteur que le triangle. Dans
la figure R ci-dessus, on voit le triangle ABC et le parallélogramme ABDC. L’aire
d’un triangle est donc égale à la moitié du produit de la base et de la
hauteur. Quand on connaît les trois côtés d’un triangle, par exemple, 25,
38 et 43 centimètres, l’aire peut se calculer ainsi :
1. On calcule le
demi-périmètre du triangle. On a : (25 + 38 + 43)/ 2 = 53.
2. On soustrait
chaque mesure de ces côtés au demi-périmètre. On a : 53 - 25 = 28, 53 -
38 = 15, 53 - 43 = 10.
3. On multiplie les
quatre résultats : On a = 53 × 28 × 15 × 10 = 222 600.
4. On extrait la
racine carrée du dernier résultat. La racine carrée de 222 600 est 471,81.
La mesure des trois angles d’un triangle est de 180
degrés. Pour le vérifier, on colorie les angles. On les découpe et on les
assemble de telle manière que les sommets se touchent.
Voici six théorèmes
concernant les triangles :
1. La somme des
mesures des angles intérieurs d'un triangle est de 180 degrés. Pour le
vérifier, on colorie les angles. On les découpe et on les assemble de telle
manière que les sommets se touchent.
2. Dans tout
triangle, la mesure d'un côté quelconque est plus petite que la somme des
mesures des deux autres côtés.
3. Dans tout
triangle, la mesure d'un côté quelconque est plus grande que la différence
des mesures des deux autres côtés.
4. Dans tout
triangle, au plus grand angle est opposé le plus grand côté.
5. L'axe de symétrie
d'un triangle isocèle supporte une médiane, une médiatrice, une bissectrice
et une hauteur de ce triangle.
6. Les axes de symétrie d'un triangle
équilatéral supportent les médianes, les médiatrices, les bissectrices et
les hauteurs de ce triangle.
© Charles-É. Jean
Index
: T
|
![]()
![]()