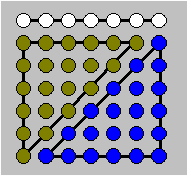
Un nombre carré peut être
représenté graphiquement par un carré ou par un triangle isocèle de points
ou de boules, comme il est illustré.
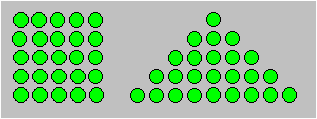
Le carré contient cinq points sur chacun de ses
côtés ; le triangle isocèle contient neuf points à la base et cinq sur
chacun des deux autres côtés. Les nombres carrés peuvent aussi être
représentés par des suites de nombres comme ceci.
|
1
= 1
1 3
= 4
1 3 5 = 9
1 3 5 7 = 16
1 3 5 7 9 = 25 |
1
= 1
1 2 1
= 4
1 2 3 2 1
= 9
1 2 3 4 3 2 1
= 16
1
2 3 4 5 4 3 2 1 = 25 |
On peut trouver la suite des carrés en utilisant un tableau.
Sur la première ligne, on écrit la suite des impairs. Sur la seconde, on
écrit la somme de deux nombres : le précédent et celui qui surmonte la
case vide suivante, comme il est illustré pour 9 + 7 = 16.
Tableau
|
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
Le rang d’un carré coïncide avec sa racine carrée. Par
exemple, comme 64 est le 8e carré, sa racine carrée est 8. On peut
écrire 82 = 64.
Proposition 3. Le terme général de la suite des
carrés est n2.
|
Démonstration
De la définition des carrés, il découle que la différence entre chacun
des termes des carrés successifs est 3, 5, 7, 9, 11, 13, ..., soit une
suite du premier degré. La suite des carrés est donc du deuxième
degré. Le terme général d’une telle suite est an2 +
bn + c. Si n = 1, on a : a + b + c
= 1 ; si n = 2, on a : 4a + 2b + c
= 4 ; si n = 3, on a : 9a + 3b + c
= 9. On résout les trois équations. On obtient : a = 1, b
= 0 et c = 0.
D’où, le terme général de la suite des carrés
est n2. |
Cela signifie que le ne carré est n2.
3. Comparaison des rangs
Proposition 4. Le carré de rang n est toujours plus grand que le
triangulaire de même rang.
|
Démonstration
Le terme général d’un carré est n2 qui est égal à
n2/2 + n2/2 ; celui d’un
triangulaire est n(n + 1)/2 qui est égal à n2/2 + n/2.
Comme n2 est plus grand que n, le carré est
toujours plus grand. |
Proposition 5. Si on divise un carré de rang n
par son rang et si on divise un triangulaire de rang n par le même rang,
la différence des deux quotients est (n - 1)/2.
|
Démonstration
Pour le carré, le rapport est n2/n = n.
Pour le triangulaire, le rapport est n(n + 1)/2n = (n
+ 1)/2. On fait : n - (n + 1)/2 = (n - 1)/2. Donc, la différence des deux quotients est (n -
1)/2. Par exemple, si n = 6, n2 = 36 et 6D
= 21. Or, 36/6 - 21/6 = 2,5. |
4. Somme de triangulaires et de carrés
Proposition 6. La somme d’un triangulaire de rang n et d’un
triangulaire de rang (n + 1) est un carré de rang (n + 1).
Formule : nD +
(n + 1)D = (n + 1)2
|
Démonstration
nD
+ (n + 1)D
n(n
+ 1)/2 +(n + 1)(n + 2)/2
(n + 1)(n
+ n + 2)/2
(n + 1)
(n + 1)
(n + 1)2 |
Illustration. 4D
+ 5D = 52
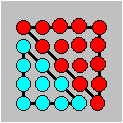
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
nD |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
|
(n + 1)D |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
|
(n + 1) 2 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
Corollaire. La différence d’un carré de rang (n +
1) et d’un triangulaire de même rang est un triangulaire de rang n.
Proposition 7. Soit 2n triangulaires
successifs, la somme des (n + 1) plus petits triangulaires successifs est
égale à la somme des (n - 1) autres triangulaires successifs. Le
premier terme de l’identité est un carré de rang n, diminué de (n
+ 1) ; le premier terme du deuxième membre de l’identité est un carré de
rang n.
Voici les premières
identités :
1D
+ 2D + 3D
= 4D
5D
+ 6D + 7D
+ 8D = 9D
+ 10D
11D
+ 12D + 13D
+ 14D + 15D
= 16D + 17D
+ 18D
19D
+ 20D + 21D
+ 22D + 23D
+ 24D = 25D
+ 26D + 27D
+ 28D
Les identités qui suivent commencent successivement par
29D,
41D, 55D,
71D, 89D,
etc. Soit r le rang de chaque identité, la somme des termes du premier
ou du deuxième membre est : (3r5 + 15r4
+ 25r3 + 15r2 + 2r)/6.
Proposition 8. Soit 2n triangulaires successifs
où n est impair à partir de 3, la somme de (n + 1)/2 carrés,
chacun étant la somme d’un couple de deux triangulaires successifs, est
égale à la somme de (n - 1)/2 carrés formés aussi par groupes de deux
triangulaires successifs. Le premier terme de l’identité exprimée en
triangulaires est 2(n - 1)D
- 1 ou n2 - n - 1 ; celui du
deuxième membre est 2(n - 1)D
+ n ou n2. Le premier terme de l’identité
exprimée en carrés est 2(n - 1)D
ou n2 - n ; celui du
deuxième membre est 2(n - 1)D
+ n + 1 ou n2 + 1.
Voici les premières
identités :
[5D
+ 6D]
+ [ 7D
+ 8D ]
= [9D
+ 10D]
62 +
82 =
102
[19D
+ 20D]
+ [21D
+ 22D]
+ [23D
+ 24D]
= [25D
+ 26D]
+ [27D
+ 28D]
202 +
222 +
242 =
262 +
282
[41D
+ 42D]
+ [43D
+ 44D]
+ [45D
+ 46D]
+ [47D
+ 48D]
= [49D
+ 50D]
+ [51D
+ 52D]
+ [53D
+ 54D]
422 +
442 +
462 +
482 =
502 +
522 +
542
Les identités qui suivent commencent successivement par 71D,
109D, 155D,
209D, 271D,
... On y trouve les termes de rang pair de la suite de la proposition
précédente.
Proposition 9. Soit (2n + 1) carrés
successifs, la somme des (n + 1) plus petits carrés successifs est
égale à la somme des n autres carrés. Le premier terme de l’identité
est le carré d’un triangulaire de rang 2n ; celui du deuxième
membre est le carré de la base du terme initial, augmentée de (n + 1).
Voici les premières
identités :
32 + 42
= 52
102 + 112
+ 122 = 132 + 142
212 + 222
+ 232 + 242 = 252 + 262 + 272
362 + 372
+ 382 + 392 + 402 = 412 + 422
+ 432 + 442
Les identités qui suivent commencent successivement par 552,
782, 1052, 1362, 1712, 2102,
... Les bases sont des triangulaires de rang pair.
Proposition 10. Soit (2n + 1) triangulaires
successifs, la somme des (n + 1) plus petits triangulaires successifs est
égale à la somme des n autres triangulaires. Le premier terme de l’identité
est le carré d’un triangulaire de rang 2n ; celui du deuxième
membre est le carré du triangulaire initial augmenté de (n + 1).
Voici les premières
identités
(2D
)2 + (2D + 1)2
= (2D + 2)2
32
+ 42 =
52
(4D
)2 + (4D + 1)2
+ (4D + 2)2 = (4D
+ 3)2 + (4D + 4)2
102
+ 112 +
122 = 132
+ 142
(6D
)2 + (6D + 1)2
+ (6D + 2)2 + (6D
+ 3)2 = (6D + 4)2
+ (6D + 5)2 + (6D
+ 6)2
212
+ 222 +
232 + 242
= 252 +
262 + 272
(8D
)2 + (8D + 1)2
+ (8D + 2)2 + (8D
+ 3)2 + (8D + 4)2
= (8D + 5)2 + (8D
+ 6)2 + (8D + 7)2
+ (8D + 8)2
362
+ 372 +
382 + 392
+ 402 =
412 + 422
+ 432 +
442
5.
Différence de triangulaire et de carrés
Proposition 11. La différence de deux triangulaires l’un de rang n
et l’autre de rang (n - 2) est égale à la différence de deux carrés
l’un de rang n et l’autre de rang (n - 1).
Formule : nD -
(n - 2)D = n2
- (n - 1)2
|
Démonstration
nD
- (n - 2)D
n(n
+ 1)/2 - (n - 2)(n - 1)/2
2n - 1
n2
- n2 + 2n - 1
n2
- (n - 1)2 |
Illustration. 5D
- 3D = 52 - 42
= 9
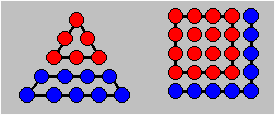
|
Tableau
|
n |
3 |
4 |
5 |
6 |
7 |
8 |
|
nD |
6 |
10 |
15 |
21 |
28 |
36 |
|
(n - 2)D |
1 |
3 |
6 |
10 |
15 |
21 |
|
Différence |
5 |
7 |
9 |
11 |
13 |
15 |
|
n 2 |
9 |
16 |
25 |
36 |
49 |
64 |
|
(n - 1)2 |
4 |
9 |
16 |
25 |
36 |
49 |
|
Différence |
5 |
7 |
9 |
11 |
13 |
15 |
Corollaire. La différence d’un carré de rang n et
d’un triangulaire de même rang est égale à la différence d’un carré de
rang (n - 1) et d’un triangulaire de rang (n - 2).
Proposition 12. La différence d’un carré de rang n
et d’un triangulaire de même rang est égale à un triangulaire de rang (n
- 1).
Formule : n2 - nD
= (n - 1)D.
|
Démonstration
n2
- nD
n2
- n(n + 1)/2
(n2
- n)/2
(n - 1)D |
Illustration. 52 - 5D
= 4D = 10
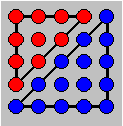
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
n 2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
nD |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
|
(n - 1)D |
0 |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
Corollaire. La somme d’un triangulaire de rang n et
d’un triangulaire de rang (n - 1) est un carré de rang n.
6. Opérations sur les multiples
Proposition 13. Tout carré de rang n diminué de son rang est égal
au double du triangulaire de rang (n - 1).
Formule : n2 - n = 2(n - 1)D
|
Démonstration
n2
- n
n(n
- 1)
2(n - 1)D
Par exemple, 52
- 5 = 20 et 2 ´ 4D
= 20. |
Illustration. 72 - 7 = 2
´
6D = 42
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
n 2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
n 2
- n |
0 |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
|
2(n - 1)D |
|
2´ 1 |
2´ 3 |
2´ 6 |
2´10 |
2´15 |
2´21 |
2´28 |
Corollaire. Tout carré de rang n est la somme de son
rang et de deux fois le triangulaire de rang (n - 1).
Proposition 14. Le double d’un triangulaire de rang n
diminué de son rang est un carré de rang n.
Formule : 2nD
- n = n2
|
Démonstration
2nD
- n
2n(n
+ 1)/2 - n
n2
|
Illustration.
2 ´ 5D - 5
= 52 = 25
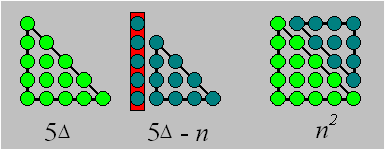
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2nD |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
72 |
|
n 2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
Corollaire. Le double d’un triangulaire de rang n
est un carré de même rang augmenté de son rang.
Proposition 15. Le double d’un triangulaire de rang n
augmenté du rang (n + 1) est un carré de rang (n + 1).
Formule : 2nD
+ (n + 1) = (n + 1)2
|
Démonstration
2nD
+ (n + 1)
2n(n
+ 1)/2 + n + 1
n2
+ 2n + 1
(n + 1)2 |
Illustration.
2 ´ 4D
+ 5 = 52 = 25
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2nD |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
72 |
|
n +
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
(n + 1)2 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
Corollaire. Le double d’un triangulaire de rang n
est égal à la différence d’un carré de rang (n + 1) et du rang de
ce carré.
Proposition 16. Le double d’un triangulaire de rang n
augmenté d’un carré de même rang est un triangulaire de rang 2n.
Formule : 2nD
+ n2 = (2n)D
|
Démonstration
2nD
+ n2
2[n(n
+ 1)/2] + n2
n2
+ n + n2
2n2
+ n
n(2n
+ 1)
2n(2n
+ 1)/2
(2n)D |
Illustration. 2 ´ 5D
+ 52 = 10D = 55
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2nD |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
72 |
|
n 2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
(2n)D |
3 |
10 |
21 |
36 |
55 |
78 |
105 |
136 |
Corollaire. Le double d’un triangulaire de rang n
est égal à la différence d’un triangulaire de rang 2n et d’un
carré de rang n.
Proposition 17. Le double d’un triangulaire de rang n
augmenté d’un carré de rang (n + 1) est un triangulaire de rang (2n
+ 1).
Formule : 2nD
+ (n + 1)2 = (2n + 1)D
|
Démonstration
2nD
+ (n + 1)2
2[n(n
+ 1)/2] + n2 + 2n + 1
2n2
+ 3n + 1
(2n + 1) (n +
1)
(2n + 1) (2n +
2)/2
(2n + 1)D |
Illustration. 2 ´ 3D
+ 42 = 7D = 28

|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2nD |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
72 |
|
(n + 1)2 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
(2n + 1)D |
6 |
15 |
28 |
45 |
66 |
91 |
120 |
153 |
Corollaire. Le double d’un triangulaire de rang n
est égal à la différence d’un triangulaire de rang (2n + 1) et d’un
carré de rang (n + 1).
Proposition 18. 1e Le triple d’un
triangulaire de rang n augmenté d’un triangulaire de rang (n -
1) est égal au double du carré de rang n augmenté de son rang.
Formule : 3nD
+ (n - 1)D = 2n2
+ n
2e Le double du carré de rang n augmenté
de son rang est égal au triangulaire de rang 2n.
Formule : 2n2 + n = (2n)D
|
Démonstration
3nD
+ (n - 1)D
3n(n
+ 1)/2 + n(n - 1)/2
(3n2
+ 3n + n2 - n)/2
(4n2
+ 2n)/2
2n2
+ n
n(2n
+ 1)
2n(2n
+ 1)/2
(2n)D |
Illustration
3 ´ 4D
+ 3D = 2
´
42 + 4 = 8D = 36

|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3nD |
3 |
9 |
18 |
30 |
45 |
63 |
84 |
108 |
|
(n - 1)D |
0 |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
|
2n2 + n |
3 |
10 |
21 |
36 |
55 |
78 |
105 |
136 |
|
(2n)D |
2D |
4D |
6D |
8D |
10D |
12D |
14D |
16D |
On déduit que le triple d’un triangulaire de rang n
augmenté d’un triangulaire de rang (n - 1) est égal au produit de n
et de (2n + 1).
7. Opérations sur les puissances
Proposition 19. Le carré du produit de deux entiers consécutifs est égal
au quadruple du carré du triangulaire de rang n.
Formule : [n(n + 1)]2 = 4(nD)2
|
Démonstration
[n(n
+ 1)]2
(2nD)2
4(nD)2 |
Exemple
Si n = 3, on a : (3 ´
4)2 = 4(3D)2
= 4 ´ 62
= 144.
|
La racine carrée de (nD)2
est nD.
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
[n(n + 1)]2 |
4 |
36 |
144 |
400 |
900 |
1764 |
3136 |
5184 |
|
4(nD)2 |
4 ´ 12 |
4 ´ 32 |
4 ´ 62 |
4 ´ 102 |
4 ´ 152 |
4 ´ 212 |
4 ´ 282 |
4 ´ 362 |
Proposition 20. Le carré de rang (2n + 1)
diminué de la somme deux carrés l’un de rang n et l’autre de rang (n
+ 1) est égal au quadruple d’un triangulaire de rang n.
Formule : (2n + 1)2 - [n2
+ (n + 1)2] = 4nD
|
Démonstration
(2n + 1)2
- [n2 + (n + 1)2]
4n2
+ 4n + 1 - n2 - n2 - 2n
- 1
2(n2
+ n)
4nD |
Exemple
Si n = 3, on a : 72 - (9 + 16) =
4 ´ 3D
= 24.
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
(2n + 1)2 |
9 |
25 |
49 |
81 |
121 |
169 |
225 |
289 |
|
n 2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
(n + 1)2 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
Somme |
5 |
13 |
25 |
41 |
61 |
85 |
113 |
145 |
|
4nD |
4 |
12 |
24 |
40 |
60 |
84 |
112 |
144 |
Corollaire. Le quadruple d’un triangulaire de rang n
augmenté de la somme de deux carrés l’un de rang n et l’autre de
rang (n + 1) est un carré de rang (2n + 1).
Proposition 21. L’octuple d’un triangulaire de
rang n augmenté de 1 est un carré de rang (2n + 1). (Diophante)
Formule : 8nD +
1 = (2n + 1)2
|
Démonstration
8nD
+ 1
8n(n
+ 1)/2 + 1
4n2
+ 4n + 1
(2n + 1)2 |
Illustration. 8 ´ 2D
+ 1 = 52 = 25

|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
8nD |
8 |
24 |
48 |
80 |
120 |
168 |
224 |
288 |
|
+ |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
(2n + 1)2 |
9 |
25 |
49 |
81 |
121 |
169 |
225 |
289 |
Corollaire. Tout carré de rang (2n + 1) diminué de 1
peut être partagé en huit triangulaires de rang n.
De la proposition 21, on peut tirer deux algorithmes qui
permettent de déterminer si un nombre est triangulaire et d’extraire la
racine triangulaire de tout nombre.
n
Premier algorithme
1. On multiplie un
nombre choisi par 8.
2. On additionne 1 au
produit.
3. On extrait la
racine carrée du résultat. Si la racine carrée est un entier, le nombre est
triangulaire.
4. On soustrait 1 à
la racine carrée.
5. On divise par 2. C’est
la racine triangulaire.
Voici deux exemples :
Prenons 153. On fait : (153 ´
8) + 1 = 1225 qui est le carré de 35. On fait 35 - 1 = 34 et 34 ¸
2 = 17. La racine triangulaire de 153 est 17. On peut écrire 17D
= 153.
Prenons 1000. On fait :
(1000 ´ 8) + 1 = 8001. La racine carrée de 8001 est
89,448. On fait 89,448 - 1 = 88,448 ; 88,448 ¸
2 = 44,224. La racine triangulaire de 1000 est 44,224. On peut
écrire 44,224D = 1000.
n
Deuxième algorithme
1. On multiplie un
nombre choisi par 2.
2. On additionne
0,25.
3. On extrait la
racine carrée. Si la racine carrée est un entier plus ½, le nombre est
triangulaire.
4. On soustrait 0,5.
C’est la racine triangulaire.
Voici deux exemples :
Prenons 153. On fait : 153 ´
2 = 306 et 306 + 0,25 = 306,25. La racine carrée de 306,25 est 17,5. On
fait : 17,5 - 0,5 = 17. La racine triangulaire de 153 est 17. On peut
écrire 17D = 153.
Prenons 1000. On fait :
1000 ´ 2 = 2000 et 2000 + 0,25 = 2000,25. La racine
carrée de 2000,25 est 44,724. On fait 44,724 - 0,5 = 44,224. On peut
écrire 44,224D = 1000.
Proposition 22. Le produit de deux triangulaires de
rangs (n - 1) et (n + 1) augmenté d’un triangulaire de rang n
est le carré d’un triangulaire de rang n.
Formule : (n - 1)D ´
(n + 1)D
+ nD
= (nD)2
|
Démonstration
(n - 1)D
´ (n + 1)D
+ nD
n(n
- 1)/2 ´ (n + 1)(n + 2)/2 + n(n
+ 1)/2
n(n
+ 1) [ (n - 1)(n + 2) + 2]/4
n(n
+ 1)2/4
(nD)2
|
Exemple
Si n = 3, on a : 2D
´ 4D
+ 3D = 3
´
10 + 6 = (3D)2 =
36
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
(n - 1)D |
0 |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
|
(n + 1)D |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
|
Produit |
0 |
6 |
30 |
90 |
210 |
420 |
756 |
1260 |
|
nD |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
|
(nD)2 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
| |
(1D )2 |
(2D)2 |
(3D)2 |
(4D)2 |
(5D)2 |
(6D)2 |
(7D)2 |
(8D )2 |
Proposition 23. La somme du carré d’un triangulaire
de rang n et du carré d’un triangulaire de rang (n + 1) est un
triangulaire de rang (n + 1)2.
Formule : (nD)2
+ [(n + 1)D]
2 = [(n + 1)2]D
|
Démonstration
(nD)2
+ [ (n + 1)D]
2
[n(n
+ 1)/2] 2 + [(n
+ 1)(n + 2)/2] 2
[(n
+ 1)2 + (2n2 + 4n + 4)]
/4
[(n2
+ 2n + 1)(n2 + 2n + 2)]/2
(n2
+ 2n + 1)
[(n
+ 1)2] D |
Exemple
Si n = 3, on a : (3D)2
+ (4D)2 = (42)D
= 136.
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
(nD)2 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
|
[(n + 1)D]
2 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
2025 |
|
Somme |
10 |
45 |
136 |
325 |
666 |
1225 |
2080 |
3321 |
|
[(n + 1)2]D |
4D |
9D |
16D |
25D |
36D |
49D |
64D |
81D |
À partir de cette proposition, on peut écrire :
(nD)2
+ [(n + 1)D]
2 = [nD
+ (n + 1)D]D
. Par exemple,
[6D]2
+ [7D]2
= [6D
+ 7D]D.
Cela revient à cette identité : 212 + 282 = 49D
= (72)D.
Proposition 24. La différence du triangulaire d’un
carré de rang n et du carré d’un triangulaire de même rang est le
carré d’un triangulaire de rang (n - 1).
Formule : (n2)D
- (nD)2 = [(n
- 1)D]
2
|
Démonstration
(n2)D
- (nD)2
n2(n2
+ 1)/2 - [n(n + 1)/2]
2
n2(n2
+ 1)/2 - n2(n2 + 2n + 1)/4
n2(n
- 1)2/4
[n(n
- 1)/2] 2
[(n
- 1)D]
2 |
Exemple
Si n = 3, on a : (32)D
- (3D)2 = (2D)2
= 9.
|
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
(n2)D |
1 |
10 |
45 |
136 |
325 |
666 |
1225 |
2080 |
|
(nD)2 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
|
(n - 1)D]
2 |
0 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
| |
0 |
1 |
32 |
62 |
102 |
152 |
212 |
282 |
.
|
Démonstration
Soit n le rang du grand carré, la somme des deux carrés est (n
- 1)2 + n2 = 2n2 - 2n
+ 1. La somme des deux triangulaires est n(n + 1)/2 + (n
+ 1)(n + 2)/2 = n2 + 2n + 1. On
fait : 2n2 - 2n + 1 = n2 +
2n + 1. On obtient n2 - 4n = 0.
D’où, n = 0 et n = 4. On exclut le 0,
car la base du premier carré serait -1. En conséquence, cette
proposition est vraie seulement pour 32 + 42 = 4D
+ 5D. |
Proposition 25. La différence du carré d’un
triangulaire de rang n et du carré d’un triangulaire de rang (n
- 1) est un cube de rang n.
Formule : (nD)2
- [(n - 1)D]2 =
n3
|
Démonstration
(nD)2
- [(n - 1)D]2
[n(n
+ 1)/2]2 - [n(n - 1)/2]2
n2[(n
+ 1)2 - (n - 1) 2 ]/4
4n3/4
n3 |
Exemple
Si n = 3, on a : (3D)2
- (2D)2 = 33
= 27.
|
Tableau
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
(nD)2 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
1296 |
|
[(n - 1)D]2 |
0 |
1 |
9 |
36 |
100 |
225 |
441 |
784 |
|
n 3 |
0 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
| |
|
2 3 |
3 3 |
4 3 |
5 3 |
6 3 |
7 3 |
8 3 |
Corollaire. La somme d’un cube de rang n et du
carré d’un triangulaire de rang (n - 1) est égal au carré d’un
triangulaire de rang n.
Proposition 26. La somme du cube du triangulaire de
rang n et du cube du triangulaire de rang (n + 1) est un multiple
du carré de rang (n + 1). Si l’un des facteurs est (n + 1)2,
l’autre est (n4 + 4n3 + 9n2
+ 10n + 4)/4. Voici un tableau qui illustre la situation :
Tableau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
[ nD]
3 |
1 |
27 |
216 |
1000 |
3375 |
9261 |
21 952 |
46 656 |
|
[(n + 1)D]
3 |
27 |
216 |
1000 |
3375 |
9261 |
21 952 |
46 656 |
91 125 |
|
Somme |
28 |
243 |
1216 |
4375 |
12 636 |
31 213 |
68 608 |
137 781 |
| |
4 ´ 7 |
9 ´ 27 |
16 ´ 76 |
25 ´ 175 |
36 ´ 351 |
49 ´ 637 |
64 ´ 1072 |
81 ´ 1701 |
Proposition 27. La somme de n cubes
consécutifs à partir de 1 est égale à un carré et la racine de ce carré
est un triangulaire de rang n.
Cette proposition peut être représentée ainsi :
(13 + 23 + 33 + 43 + ... + n3)
= (1 + 2 + 3 + 4 + ... + n)2 = (nD)2
Voici un tableau qui illustre la situation :
Tableau
|
Multiplication |
Somme S |
Ö S |
Rang du D |
|
13 |
1 |
1 |
1 |
|
13 + 23 |
9 |
3 |
2 |
|
13 + 23 + 33 |
36 |
6 |
3 |
|
13 + 23 + 33 + 43 |
100 |
10 |
4 |
|
13 + 23 + 33 + 43
+ 53 |
225 |
15 |
5 |
.
|
Démonstration
La proposition
est vérifiée pour n qui varie de 1 à 5.
On pose p(k)
= (13 + 23 + 33 + 43 + ... + k3)
= (kD)2
On suppose que
p(k) est vraie. Alors, p(k + 1)
= (13 + 23 + 33 + 43 + ... + k3
+ (k + 1)3
= [(k +
1)D]2
= [(k +
1)(k + 2)/2]2
Ce qui
équivaut à dire que p(k + 1) est vraie car kD
= k(k + 1)/2.
|
Proposition 28. La somme 30 + 32
+ 34 + 36 + ... + 32n est un
triangulaire de rang (30 + 31 + 32
+ 33 + ... + 3n)
Tableau
|
n |
Multiplication |
Somme S |
Rang du D |
|
|
|
0 |
30 |
1 |
1 |
1 |
30 |
|
1 |
30 + 32 |
10 |
4 |
1 + 3 |
30 + 31 |
|
2 |
30 + 32 + 34 |
91 |
13 |
1 + 3 + 9 |
30 + 31 + 32 |
|
3 |
30 + 32 + 34 + 36 |
820 |
40 |
1 + 3 + 9 + 27 |
30 + 31 + 32 + 33 |
|
4 |
30 + 32 + 34 + 36
+ 38 |
7381 |
121 |
1 + 3 + 9 + 27 + 81 |
30 + 31 + 32 + 33
+ 34 |
La différence entre deux triangulaires successifs est un
carré.
8. Paires de triangulaires dont l’un est le double de l’autre
Proposition 29. Il existe une infinité de nombres triangulaires dont l’un
est le double de l’autre.
On illustre cette proposition par le tableau ci-dessous dans
lequel les lettres de la première colonne sont explicitées. Sur les lignes F
et G, on trouve deux suites de paires de nombres triangulaires dont l’un est
le double de l’autre.
A. Rang n des
termes qui permettent de trouver ces nombres
B. Le double du
carré de A diminué de 1, soit 2n2 - 1. Le résultat est un
carré.
C. Racine carrée de
B
D. Moitié de A
diminuée de 1. Ce nombre est le rang d’un terme triangulaire.
E. Moitié de C
diminuée de 1. Ce nombre est le rang d’un terme triangulaire.
F. Triangulaire de
rang donné en D
G. Triangulaire de
rang donné en E
Tableau
|
A |
1 |
5 |
29 |
169 |
985 |
5741 |
33 461 |
A001653 |
|
B |
1 |
49 |
1681 |
57 121 |
1 940 449 |
65 918 161 |
2 239 277 041 |
A008843 |
|
C |
1 |
7 |
41 |
239 |
1393 |
8119 |
47 321 |
A002315 |
|
D |
- |
2 |
14 |
84 |
492 |
2870 |
16 730 |
A053141 |
|
E |
- |
3 |
20 |
119 |
696 |
4059 |
23 660 |
A001652 |
|
F |
- |
3 |
105 |
3570 |
121 278 |
4 119 885 |
139 954 815 |
A075528 |
|
G |
- |
6 |
210 |
7140 |
242 556 |
8 239 770 |
279 909630 |
A029549 |
On a les couples suivants de triangulaires dont le deuxième
est le double du premier : (3, 6), (105, 210), (3570, 7140), etc. Le code
de la colonne de droite provient du site The On-Line Encyclopedia of Integer
Sequences de N. J. A. Sloane. La suite 48, 1680, 57 120, 1 940 448, 65 918
160, ... (A008845) est à l’origine de ces relations. Si on additionne 1 à sa
moitié, on obtient un carré. Par exemple, 24 + 1 = 25, le carré de 5 (A). Si
on lui additionne 1, on obtient un autre carré. Par exemple, 48 + 1 = 49, le
carré de 7 (C).
Chaque nombre de la suite A à partir de 5 s’obtient en
multipliant par 6 le nombre précédent et en soustrayant le nombre antérieur.
Par exemple, 5 ´ 6 - 1 = 29, 29
´
6 - 5 = 169, 169 ´ 6 - 29 = 985, 985
´
6 - 169 = 5741, ... Les termes de la suite C s’obtiennent comme pour la A. Par
exemple, on écrit : 7 ´ 6 - 1 = 41, 41
´
6 - 7 = 239, 239 ´ 6 - 41 = 1393, 1393
´
6 - 239 = 8119. Les nombres de cette suite sont tous impairs.
9. Les triangulaires carrés
Proposition 30. Lorsque xD
= y2, alors (3x + 4y + 1)D
est en même temps triangulaire et carré. Par exemple, lorsque 49D
= 352, alors 41 616 est un triangulaire de rang 288 et un carré de
rang 204.
Tableau
|
xD |
y 2 |
xD =
y2 |
(3x + 4y + 1)D |
|
|
1D |
12 |
1 |
8D |
62 |
|
8D |
62 |
36 |
49D |
352 |
|
49D |
352 |
1225 |
288D |
2042 |
|
288D |
2042 |
41 616 |
1681D |
11892 |
|
1681D |
11892 |
1 413 721 |
9800D |
69302 |
Cette proposition a été établie par Warclaw Sierpinski en
1961.
Proposition 31. Soit l’équation de Pell : 8x2
+ 1 = y2, lorsqu’on remplace x dans cette équation
et que le résultat est un carré, alors x2 est un
triangulaire et son rang est (y - 1)/2.
Tableau
|
x 2 |
y 2 |
x 2 |
rang du D |
|
12 |
32 |
1 |
1 |
|
62 |
172 |
36 |
8 |
|
352 |
992 |
1225 |
49 |
|
2042 |
5772 |
41 616 |
288 |
|
11892 |
33632 |
1 413 721 |
1681 |
Des propositions 30 et 31, on peut conclure qu’il existe
une infinité de nombres qui sont à la fois triangulaires et carrés
10. Applications
Proposition 32. Dans tout carré magique d’ordre 3, la somme des carrés
des éléments de la première ligne est égale à la somme des carrés des
éléments de la troisième ligne. Cela est vrai aussi pour la somme des
éléments de la première et de la troisième colonne. Soit le carré magique,
On peut établir le
système d’équations suivant :
A + B + C = D + E + F
A2 + B2
+ C2 = D2 + E2 + F2
Dans le carré magique suivant,
On a donc :
18 + 6 + 15 = 11 + 20
+ 8 = 39
182 + 62
+ 152 = 112 + 202 + 82 = 585
Les deux couples
sont : (6, 15, 18) et (8, 11, 20).
Pour démontrer cette proposition, on prend un carré magique
général comme celui-ci.
|
a |
-a - b |
b |
|
-a + b |
0 |
a - b |
|
-b |
a + b |
-a |
On peut
écrire :
a + (-a - b)
+ b = -b + (a + b) + (-a) = 0
a2 +
(-a - b)2 + b2 = (-b)2
+ (a + b)2 + (-a)2 = 2(a2
+ ab + b2)
Proposition 33. Dans tout carré magique d’ordre 3,
la somme des triangulaires des éléments de la première ligne est égale à la
somme des triangulaires des éléments de la troisième ligne. Cela est vrai
aussi pour la somme des éléments de la première et de la troisième colonne.
En s’inspirant du
cas précédent, on peut établir le système d’équations suivant :
A + B + C = D + E + F
AD
+ BD + CD
= DD + ED
+ FD
On peut
écrire :
a + (-a - b)
+ b = -b + (a + b) + (-a) = 0
aD
+ (-a - b)D
+ bD
= (-b)D
+ (a + b)D
+ (-a)D
= a2 + ab + b2
Dans le carré donné précédemment, on a :
18 + 6 + 15 = 11 + 20
+ 8 = 39
18D
+ 6D + 15D
= 11D + 20D
+ 8D = 312
Les deux triplets sont : (6, 15, 18) et (8, 11, 20). Ce
sont les mêmes triplets que pour les carrés.
Nous conjecturons que cette règle s’applique à tous les
nombres polygonaux. On pourrait l’exprimer ainsi.
Dans tout carré magique d’ordre 3, la somme des polygonaux (triangulaires,
carrés, pentagonaux, hexagonaux, etc.) des éléments de la première ligne est
égale à la somme des mêmes polygonaux des éléments de la troisième ligne.
Cela est vrai aussi pour la somme des éléments de la première et de la
troisième colonne.
Proposition 34. Dans certains carrés magiques d’ordre
4, la somme des carrés d’une rangée peut être égale à la somme des
carrés d’une autre rangée.
|
3 |
6 |
9 |
16 |
|
13 |
12 |
7 |
2 |
|
8 |
1 |
14 |
11 |
|
10 |
15 |
4 |
5 |
Dans ce carré magique, on peut établir notamment les identités
suivantes :
Lignes 1 et 3 : 3D
+ 6D + 9D
+ 16D = 8D
+ 1D + 14D
+ 11D = 208
32
+ 62 + 92 + 162
= 82 + 12
+ 142 + 112
= 382
Lignes 2 et 4 :
13D + 12D
+ 7D + 2D
= 10D + 15D
+ 4D + 5D
= 200
132
+ 122 + 72 + 22
= 102 + 152
+ 42 + 52
= 366
Colonnes 1 et
3 : 3D
+ 13D + 8D
+ 10D = 9D
+ 7D + 14D
+ 4D = 188
32
+ 132 + 82
+ 102 = 92
+ 72 + 142
+ 42 = 342
Colonnes 2 et
4 : 6D
+ 12D + 1D
+ 15D = 16D
+ 2D + 11D
+ 5D = 220
62
+ 122 + 12
+ 152 = 162
+ 22 + 112
+ 52 = 406
Colonne 2 et
diagonale 2 : 6D
+ 12D + 1D
+ 15D = 1D
+ 7D + 10D
+ 16D = 220
62
+ 122 + 12
+ 152 = 12
+ 72 + 102 +
162 = 406
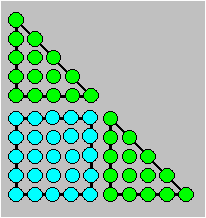
Proposition 35. Dans la représentation d’un
triangulaire, lorsque les points sont reliés les uns aux autres par des droites
horizontales et obliques, le nombre de triangles unitaires est un carré. Si le
triangulaire est de rang n, le carré est de rang (n - 1), soit (n
- 1)2.
En effet, à partir du sommet, on compte 1, 3, 5, 7, ...
triangles. Or, la somme des nombres impairs consécutifs est un carré. Dans le
triangulaire de rang 5 suivant, on compte 16 triangles unitaires.
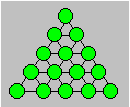
Proposition 36. Dans une grille carrée n
´
n, le nombre de rectangles, en incluant les carrés, est le carré d’un
nombre triangulaire de rang n. La formule est : [n(n +
1)/2]2.
Dans une grille 4 ´ 4, on peut
compter [4(4 + 1)/2]2 = 100 rectangles. La répartition se fait
ainsi :
Tableau
| |
1 ´ 1 |
1 ´ 2 |
1 ´ 3 |
1 ´ 4 |
2 ´ 2 |
2 ´ 3 |
2 ´ 4 |
3 ´ 3 |
3 ´ 4 |
4 ´ 4 |
|
Rectangles |
16 |
24 |
16 |
8 |
9 |
12 |
6 |
4 |
4 |
1 |
En guise de conclusion
Nous avons arrêté notre recherche à la proposition 36. Ce nombre est à
la fois un triangulaire et un carré. Le nombre de relations que nous avons
découvertes peut paraître surprenant ; mais cela découle du fait qu’un
triangulaire est un demi-carré moins le demi-rang de ce dernier. Dès le
départ, il existe entre les deux classes de nombres un lien très serré. On
peut penser que de nombreuses autres propositions pourraient davantage
rapprocher ces deux classes de nombres. Û
![]()
![]()