Série A

Solution 77

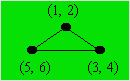Il y a trois couples de chatons qui ne doivent pas être voisins : (1, 2), (3, 4), (5, 6). On trace un triangle et on fait correspondre à chaque sommet un de ces couples. En commençant par 1, on pourra trouver toutes les dispositions.

On se déplace sur les côtés du triangle en revenant en arrière au besoin et en choisissant l’un ou l’autre des chatons d’un couple. Voici les 16 dispositions possibles :

Retour au problème

Série B

Solution 77

En tout, Siméon a rassemblé cinq sacs de pommes vertes et cinq sacs de pommes rouges, soit un total de 65 pommes. Il y a donc 13 pommes en tout dans deux sacs, l’un de pommes vertes et l’autre de pommes rouges. Comme la différence entre la quantité totale de pommes pour les deux jours est 3, elle est aussi 3 entre deux sacs de pommes de couleurs différentes. On cherche deux nombres dont la somme est 13 et dont la différence est 3. Ces nombres sont 5 et 8. 

Il y a huit pommes rouges par sac.

Retour au problème

Série C

Solution 77

Soit x, y, z et t les valeurs des jetons. On peut écrire : 4x + 16y + 64z + 256t = 908. En divisant l’équation par 4, on obtient : x + 4y + 16z + 64t = 227. Si on divise 227 par 4, le reste est 3. L’enfant qui a la grille 2 ´ 2 a le jeton 3, à cause du x qui n’a pas de coefficient. 

On peut écrire : 4y + 16z + 64t = 224. En divisant l’équation par 4, on obtient : y + 4z + 16t = 56. Si on divise 56 par 4, le reste est 0. L’enfant qui a la grille 4 ´ 4 a le jeton 4. 

On peut écrire : 4z + 16t = 52. En divisant l’équation par 4, on obtient : z + 4t = 13. Si on divise 13 par 4, le reste est 1. L’enfant qui a la grille 8 ´ 8 a le jeton 5. Il reste le jeton 2 pour la grille 16 × 16. Le tableau illustre la situation pour chaque enfant :

Retour au problème