° Nombre heptagonal. – Nombre polygonal qui est engendré par un heptagone régulier. Tout nombre de rang n de cette classe est la somme des n premiers gnomoniques heptagonaux. Le terme général est n(5n - 3)/2. Les quatre plus petits heptagonaux peuvent être représentés ainsi :

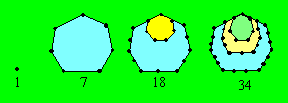
Un heptagonal de rang n peut aussi être représenté comme un trapézoïdal formé de n lignes de points et dont la base contient (3n - 2) points. 

Un nombre est heptagonal si on peut décomposer son double en deux facteurs : un entier et le quintuple de cet entier moins 3. Le plus petit facteur est le rang de l’heptagonal. Pour trouver son successeur, on lui additionne cinq fois son rang et 1. Par exemple, 403 est un heptagonal car 403 × 2 = 13 × (5 × 13 - 3). Il est de rang 13. Son successeur est 403 + (5 × 13) + 1 = 469. 

Les 59 plus petits heptagonaux sont :

Voici quelques propriétés concernant les nombres de cette classe :

La période des unités des nombres successifs correspond à un nombre de 20 chiffres : 17 845 128 956 239 067 340.

La somme des n premiers heptagonaux est un pyramidal heptagonal de rang n.

La différence de deux heptagonaux successifs est un gnomonique heptagonal.

Tout heptagonal est la différence de deux pyramidaux heptagonaux successifs.

Tout entier est heptagonal ou est la somme d’au moins deux et d’au plus sept heptagonaux. (Fermat)

Quarante fois un heptagonal de rang n plus 9 est un carré de rang (10n - 3).

L’ensemble des heptagonaux forme une suite arithmétique de degré 2.

Selon Ozanam (1640-1717), si on multiplie un heptagonal par 40 et qu’on ajoute 9 au produit, la somme est un carré. La racine carrée appartient à la suite : 7, 17, 27, 37, etc.