Dictionnaire de mathématiques récréatives Aiguilles

Aiguilles
1^e Objet usuel qui apparaît sur le cadran d'une montre ou d'une horloge et qui permet la formulation de récréations. L’aiguille des heures, appelée communément petite aiguille, repose sur 12 divisions significatives qui sont marquées de 1 à 12. L’aiguille des minutes, appelée grande aiguille, repose sur 60 divisions, tout comme celle des secondes.

Des récréations touchent aux positions des aiguilles les unes par rapport aux autres et au dérèglement du mécanisme qui entraîne des retards et des avances sur l’heure exacte. Voici quatre problèmes récréatifs :

Récréation 1. Quand les aiguilles d’une horloge ou d’une montre sont-elles superposées ?

Les aiguilles sont superposées à 0 heure. L’aiguille des minutes parcourt 60 divisions pendant que celle des heures en parcourt cinq. À chaque heure, l’aiguille des minutes parcourt 55 divisions de plus que celle des heures. Pour atteindre une division, il est nécessaire que l’aiguille des minutes parcoure 12/11 de minute. Pour atteindre cinq divisions, l’aiguille des heures avance de 60/11 d’heure ou de cinq minutes et 5/11 à chaque heure. Entre chaque superposition, le temps écoulé est d’une heure 5 minutes et 5/11. Sur le cadran, les aiguilles sont superposées 11 fois, soit aux moments suivants.

Avec fractions ordinaires	Avec secondes
1 h 05 et 5/11 min	1 h 05 min 27 s
2 h 10 et 10/11 min	2 h 10 min 54 s
3 h 16 et 4/11 min	3 h 16 min 22 s
4 h 21 et 9/11 min	4 h 21 min 49 s
5 h 27 et 3/11 min	5 h 27 min 16 s
6 h 32 et 8/11 min	6 h 32 min 43 s
7 h 38 et 2/11 min	7 h 38 min 11 s
8 h 43 et 7/11 min	8 h 43 min 38 s
9 h 49 et 1/11 min	9 h 49 min 05 s
10 h 54 et 6/11 min	10 h 54 min 32 s
12 h 00	12 h 00

Récréation 2. Quand les aiguilles d’une horloge ou d’une montre sont-elles opposées ?

Après 0 h, les aiguilles sont opposées quand l’aiguille des minutes a parcouru 6/11 d’heure ou 32 minutes et 8/11. Les aiguilles sont opposées 32 minutes et 8/11 après leur dernière superposition ou encore une heure cinq minutes et 5/11 après leur dernière opposition. Sur le cadran, les aiguilles sont opposées 11 fois, soit aux moments suivants.

Avec fractions ordinaires	Avec secondes
0 h 32 et 8/11 min	0 h 32 min 43 s
1 h 38 et 2/11 min	1 h 38 min 11 s
2 h 43 et 7/11 min	2 h 43 min 38 s
3 h 49 et 1/11 min	3 h 49 min 05 s
4 h 54 et 6/11 min	4 h 54 min 32 s
6 h 00	6 h 00
7 h 05 et 5/11 min	7 h 05 min 27 s
8 h 10 et 10/11 min	8 h 10 min 54 s
9 h 16 et 4/11 min	9 h 16 min 22 s
10 h 21 et 9/11 min	10 h 21 min 49 s
11 h 27 et 3/11 min	11 h 27 min 16 s

On pourrait obtenir ce tableau en additionnant ou en soustrayant six heures aux données du premier tableau de façon à demeurer dans l’intervalle de 0 à 12 heures. Voici une illustration de la position des aiguilles :

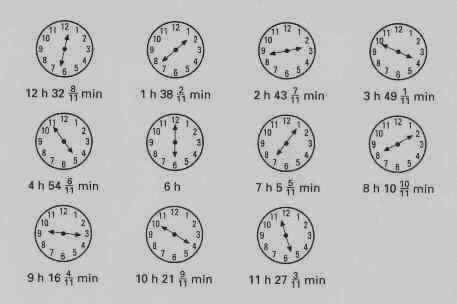
Récréation 3. Quand les aiguilles d’une horloge ou d’une montre sont-elles à angles droits ?

3.1 La grande aiguille dépasse la petite
Après 0 h, les aiguilles sont à angles droits quand l’aiguille des minutes a parcouru 3/11 d’heure ou 16 minutes et 4/11. Les aiguilles sont à angles droits 16 minutes et 4/11 après leur dernière superposition ou encore une heure cinq minutes et 5/11 après leur dernière position angulaire. Dans ce cas, sur le cadran, les aiguilles sont à angles droits 11 fois, soit aux moments suivants.

Avec fractions ordinaires	Avec secondes
0 h 16 et 4/11 min	0 h 16 min 22 s
1 h 21 et 9/11 min	1 h 21 min 49 s
2 h 27 et 3/11 min	2 h 27 min 16 s
3 h 32 et 8/11 min	3 h 32 min 43 s
4 h 38 et 2/11 min	4 h 38 min 11 s
5 h 43 et 7/11 min	5 h 43 min 38 s
6 h 49 et 1/11 min	6 h 49 min 05 s
7 h 54 et 6/11 min	7 h 54 min 32 s
9 h 00	9 h 00
10 h 05 et 5/11 min	10 h 05 min 27 s
11 h 10 et 10/11 min	11 h 10 min 54 s

On pourrait obtenir ce tableau en additionnant neuf heures ou en soustrayant trois heures aux données du tableau de la première récréation de façon à demeurer dans l’intervalle de 0 à 12 heures.

3.2 La grande aiguille précède la petite
On obtient autant de positions des aiguilles que dans le cas précédent. Il suffit d’ajouter ou de retrancher six heures aux données du tableau précédent de façon à demeurer dans l’intervalle de 0 à 12 heures. On obtiendra :

Avec fractions ordinaires	Avec secondes
0 h 49 et 1/11 min	0 h 49 min 05 s
1 h 54 et 6/11 min	1 h 54 min 32 s
3 h 00	3 h 00
4 h 05 et 5/11 min	4 h 05 min 27 s
5 h 10 et 10/11 min	5 h 10 min 54 s
6 h 16 et 4/11 min	6 h 16 min 22 s
7 h 21 et 9/11 min	7 h 21 min 49 s
8 h 27 et 3/11 min	8 h 27 min 16 s
9 h 32 et 8/11 min	9 h 32 min 43 s
10 h 38 et 2/11 min	10 h 38 min 11 s
11 h 43 et 7/11 min	11 h 43 min 38 s

Bref, sur le cadran, les aiguilles sont à angles droits 22 fois.

Récréation 4. À quelle heure l’aiguille des minutes est en avant de celle des heures de la distance que cette dernière devance le chiffre 12 sur le cadran ? (Problème posé par le mathématicien russe Yakov Pérelman (1882-1942) dans Expériences et problèmes récréatifs. Éditions Mir, 1974, p. 295) Voir solution 4

2^e Buffon a imaginé une situation où, en jetant des aiguilles sur le plancher, on peut obtenir une valeur rapprochée de p.

Index : A