1^e Objet usuel qui permet la formulation de récréations. L'horloge peut être à aiguilles ou à affichage numérique. Différents éléments de l'horloge peuvent être utilisés comme problèmes récréatifs : le tintement, la disposition des aiguilles, le cadran avec ses chiffres romains ou arabes, le dérèglement du mécanisme amenant des retards ou des avances, le dateur, la coïncidence d'affichage de chiffres semblables. Deux problèmes récréatifs sont donnés ci-après. Le second peut convenir aussi à la montre.

Récréation 1. Une pendule ne sonne que les heures. Combien sonne-t-elle de coups en 24 heures ? (Frères de l’Instruction Chrétienne. Cours d’algèbre élémentaire, no 1885) Voir solution 1 

Récréation 2. Hier, j’ai vérifié ma pendule et mon réveil : je les ai mis à l’heure. La pendule retarde de deux minutes et le réveil avance d’une minute par heure. Aujourd’hui, ils se sont arrêtés, les ressorts n’étant pas remontés. Les aiguilles indiquent 7 h sur le cadran de la pendule, et 8h sur celui du réveil. À quelle heure ai-je vérifié les montres hier ? (Problème posé par Yakov Pérelman (1882-1942) dans Expériences et problèmes récréatifs. Éditions Mir, 1974 p. 293) Voir solution 2

Lewis Carroll a proposé un problème sur le fonctionnement de l'horloge. 

2^e Diagramme en forme d'horloge qui permet d'illustrer la période d'un nombre décimal périodique. Il s'agit de lire les nombres sur le cadran dans le sens conventionnel et cela, à partir de n'importe quel chiffre. Lorsque le nombre de chiffres de la période est inférieur d'une unité au dénominateur de la fraction correspondante, on a une seule horloge. Dans les autres cas, le nombre d'horloges correspond au dénominateur, moins l'unité, de la fraction sur le nombre de chiffres d'une période. 

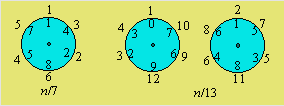
L'horloge de gauche représente la période de la fraction n/7 lorsque n varie de 1 à 6. Le nombre extérieur est le numérateur n de la fraction à l'endroit où la période commence. Ainsi, la période de 3/7 est 428 571 et celle de 4/7 est 571 428. Les deux autres horloges représentent les deux parties de la fraction n/13 lorsque n varie de 1 à 12. Par exemple, la période de 4/13 est 307 692 et celle de 7/13 est 538 461.

L'horloge arithmétique peut être considérée comme un diagramme. 

© Charles-É. Jean

Index : H