|
Âge
2. Cette personne est née en 1981 ; elle
a eu 19 ans en 2000.
3. Les âges respectifs sont 4 ans, 8 ans et 48 ans.
4. L’amateur
de casse-tête a 18 ans.
5. Il est
mort à 33 ans et son règne a duré 12 ans.
Retour au texte
Aiguilles
4. L’aiguille des heures a dépassé le
chiffre 12 de 1/10 de tour complet, ce qui demande 12/10 d’heure ou 1 h 12
min. À ce moment, l’aiguille des minutes sera deux fois plus éloignée du
12, c’est-à-dire à une distance égale à 1/5 de tour. Pour une période de
12 heures, les aiguilles sont superposées aux moments suivants.
|
1 h 12 min |
2 h 24 min |
3 h 36 min |
4 h 48 min |
6 h |
|
7 h 12 min |
8 h 24 min |
9 h 36 min |
10 h 48 min |
12 h |
Retour au texte
Astérithme
1. L'identité est : 417 × 21 921
= 9 141 057.
2. Les identités possibles sont : 324 + 765 = 1089, 357 + 849 =
1206, 364 + 725 = 1089, 743 + 859 = 1602.
3. L’identité est : 75 321 + 12 357 = 87 678.
Retour au texte
Boule
Ce nombre est 80.
Retour au texte
Chou
Le batelier transporte la chèvre puis
revient chercher le chou ou le loup. Il ramène la chèvre. Il prend ensuite le
loup ou le chou. Enfin, il revient chercher la chèvre.
Voici une façon de déplacer les cartes : On
prend le 2, un 6 et le 7 qu’on amène à l'îlot B. On ramène le 7 à l'îlot
A. On prend le 3, le 5 et le 7 qu’on amène à l'îlot B. On ramène le 5 à
l'îlot A. On prend le 4, le 5 et le 6 qu’on amène à l'îlot B.
Retour au texte
Croisés
(Nombres)
Les trois grilles remplies sont :
|
1 |
G |
H |
I |
J |
K |
L |
|
2 |
G |
H |
I |
J |
K |
L |
|
3 |
G |
H |
I |
J |
K |
L |
|
A |
5 |
7 |
8 |
|
9 |
9 |
|
A |
1 |
6 |
9 |
2 |
|
7 |
|
A |
7 |
2 |
|
6 |
8 |
5 |
|
B |
3 |
2 |
7 |
|
5 |
4 |
|
B |
4 |
3 |
|
5 |
4 |
8 |
|
B |
7 |
9 |
1 |
|
4 |
1 |
|
C |
8 |
9 |
|
5 |
3 |
|
|
C |
|
4 |
9 |
5 |
|
6 |
|
C |
7 |
|
3 |
6 |
1 |
8 |
|
D |
|
4 |
5 |
8 |
|
1 |
|
D |
4 |
5 |
|
6 |
5 |
4 |
|
D |
6 |
3 |
6 |
6 |
|
4 |
|
E |
2 |
|
3 |
5 |
5 |
6 |
|
E |
2 |
|
7 |
|
0 |
|
|
E |
|
2 |
9 |
6 |
3 |
|
|
F |
5 |
4 |
3 |
|
5 |
2 |
|
F |
8 |
4 |
2 |
|
8 |
8 |
|
F |
1 |
8 |
|
6 |
7 |
0 |
(Problème 3) À partir des expressions divisibles et de celles élevées au carré, on
trouve que a = 72, b = 29, c = 18, d = 37.
Retour au texte
Cryptarithme
a)
138 × 138 = 19 044
b) 1256
c) On fait la somme
des trois égalités. On obtient : 2A + 2B + 2C = 42. On divise par 2. On
a : A + B + C = 21.
Retour au texte
Cryptarithmique
(Récréation)
Sim a compté 585
grenouilles.
Retour au texte
Cure-dents
a) Ce nombre est 20.
b) Si les 10 hexagones étaient non
adjacents, on aurait 60 cure-dents. Or, 18 cure-dents appartiennent à deux
hexagones. Martine devra utiliser 42 cure-dents.
Retour au texte
Devinette
a) Le grand-père est avec son fils
qui est aussi le père du plus jeune.
b) A
est âgé de 54 ans, B de 45 ans et C de 4 ans et demi.
Retour
au texte
Division
1. Le nombre est 2519.
2.
Le marchand a 119 pommes.
3. Le berger a 727 moutons.
Retour
au texte
Ennéadigitale
(Identité)
Quatre égalités sont possibles : 192 + 384 = 576, 219 + 438 = 657,
273 + 546 = 819, 327 + 654 = 981.
Retour au texte
Gain
On commence par la fin. Chaque joueur possède 120 pistoles.
Puisque C fut le dernier perdant, avant le 3e jeu, les autres avaient
alors chacun 60 pistoles, soit la moitié de 120. C avait la différence, soit
360 - (2 ´ 60) = 240 pistoles. On continue ainsi
comme l’indique le tableau.
| |
A |
B |
C |
|
Avant le 1er jeu |
195 |
105 |
60 |
|
Avant le 2e jeu |
30 |
210 |
120 |
|
Avant le 3e jeu |
60 |
60 |
240 |
|
À la fin |
120 |
120 |
120 |
Au début, A avait 195 pistoles, B 105 pistoles et C 60
pistoles.
Retour au texte
Horloge
1. La pendule sonne ses coups de 1 à 12,
puis recommence. On aura donc deux fois la somme des nombres de 1 à 12. L’horloge
sonne 156 coups en 24 heures.
2. Le réveil avance de 3
minutes en une heure par rapport à la pendule. En 20 heures, il avancera d’une
heure, c’est-à-dire de 60 minutes. Mais pendant ces 20 heures, le réveil a
devancé le temps exact de 20 minutes. Donc, les aiguilles étaient remises
à l’heure il y a 19 h 20 min, c’est-à-dire à 11 h 40 min.
Retour au texte
Jeton
Un carré rempli est :
Retour au texte
Lettre
La somme des expressions de la troisième ligne est 3B et est égale
à 21. D'où B = 7. En remplaçant B par sa valeur dans la deuxième colonne, on
trouve que A = 5. Dans la quatrième colonne, en remplaçant A et B par leur
valeur, on trouve que C = 2. La grille complétée est :
|
12 |
5 |
7 |
14 |
|
7 |
19 |
2 |
2 |
|
2 |
7 |
5 |
7 |
|
11 |
2 |
3 |
17 |
Retour au texte
Magique (Rectangle)
Une disposition est :
Retour au texte
Mathématique
(Récréation)
a) 20 et 28
b) 20 et 28 casseaux
c) 20 et 28 ans
d) 20 et 28 paniers
de pommes
e) 20 et 28 fusées
Retour au texte
Nombre (Grand)
Ce nombre est 1010 élevé
à la puissance 10. L’expression 1010 est égale à 10 milliards. D’où,
ce nombre est égal à l suivi de 10 milliards de 0.
Retour au texte
Parenté
2. Jacques achète 7 livres, Louis 4 livres, Pierre 8 livres, André 1 livre.
André est le fils de Louis et Jacques le fils de Pierre.
Retour
au texte
Partage
Le garagiste a fait une erreur de calcul, car :
1/6 + 1/5 + 1/4 + 1/3 = 114/120 = 95 % et non 100 %.
Retour au texte
Poids
Puisque le poids de chaque bille est exprimé en
nombres entiers, on peut identifier les combinaisons possibles pour chaque
boîte.
|
18 grammes |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
|
Nombre de billes |
1 |
2 |
3 |
6 |
9 |
18 |
|
Poids en grammes |
18 |
9 |
6 |
3 |
2 |
1 |
|
32 grammes |
(7) |
(8) |
(9) |
(10) |
(11) |
(12) |
|
Nombre de billes |
1 |
2 |
4 |
8 |
16 |
32 |
|
Poids en grammes |
32 |
16 |
8 |
4 |
2 |
1 |
|
54 grammes |
(13) |
(14) |
(15) |
(16) |
(17) |
(18) |
(19) |
(20) |
|
Nombre de billes |
1 |
2 |
3 |
6 |
9 |
18 |
27 |
54 |
|
Poids en grammes |
54 |
27 |
18 |
9 |
6 |
3 |
2 |
1 |
On élimine les combinaisons dont le nombre de billes est
supérieur à 13 ou dont le poids est supérieur à 52 grammes, c’est-à-dire
6, 11, 12, 13, 18, 19 et 20. Il s’agit de combiner les billes de chaque boîte
de telle sorte qu’il y ait 13 billes en tout et que le poids des trois billes
(une bille par boîte) soit de 52 grammes. Les boîtes contiennent neuf
billes de 2 grammes, une bille de 32 grammes et trois billes de 18 grammes.
Retour au texte
Renversé (Nombre)
1. Si on additionne un certain nombre
de deux chiffres et
son renversé, le résultat est toujours un multiple de 11. De plus, le facteur
de 11 correspond à la somme des chiffres du nombre de départ (ou de son
renversé). Exemple : 24 + 42 = 66 = 11 ´
6.
Les multiples de 11 entre 54 et 90 sont 55, 66, 77 et 88. Seuls 66 et 88 sont
pairs. Si la somme était 66, il faudrait que le nombre cherché soit situé
entre 54 et 66. Aucun nombre impair de cet intervalle ajouté à son nombre
renversé ne donne 66. La somme est donc 88. Or, 71 + 17 = 88, 62 + 26 = 88, 53
+ 35 = 88. Le nombre cherché est 71.
2. Les nombres qui restent sont 43 et 61. Le
nombre-clef est 104.
3. Le nombre cherché est 2178.
Retour au texte
Résiduaire
(Partage)
M a distribué 64 bouteilles de vin.
Retour au texte
Ternaire (Numération)
Après CBA, on peut écrire :
CBB, CBC, CCA, CCB, CCC, BAAA, BAAB, BAAC, BABA, BABB, BABC. D’où, BABC correspond
à 32.
Après BABC, on peut écrire :
BACA, BACB, BACC, BBAA, BBAB, BBAC, BBBA, BBBB. D’où, 40 correspond à BBBB.
Retour au texte
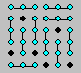
Trait
Voici une façon de relier les points bleus :
Retour au texte
|
![]()
![]()