Billard
1^e Objet de récréations. La table de billard est représentée par une grille constituée de carrés unitaires ayant une forme et des mesures variées. Un mobile se déplace sur les diagonales en s'inspirant du principe du déplacement d'une bille au jeu de billard. La grille peut être trouée dans ses coins et même sur les bordures. 

Dans chacune des figures suivantes, un mobile qui part du point en se dirigeant vers la droite suivra le chemin indiqué pour revenir au point de départ.

Le mobile a touché à 35 points d'intersection dans la première figure. Il a suivi 30 diagonales des carrés unitaires dans l'autre figure. 

Un mobile qui part du coin A sur une table 4 × 7 fait neuf rebonds sur la bande avant d’atteindre le coin B. Lorsque les nombres représentant les mesures sont premiers entre eux, le nombre de rebonds est égal à la somme des mesures de la longueur et de la largeur à laquelle on soustrait 2, ce qui donne 7 + 4 - 2 = 9.

Dans cet exemple, on compte 40 sommets. Deux sommets marquent le départ et l’arrivée du mobile. 

Soit les points (p, q) où p est le rang de la ligne et q le rang de la colonne, le mobile passe par les points où (p + q) est paire. Soit s le nombre de sommets, un mobile passe par (s - 2)/2 sommets. Dans l’exemple donné, le mobile passe par (40 - 2)/2 = 19 sommets, si on exclut les points de départ et d’arrivée. 

Les récréations consistent à trouver le chemin d'un mobile qui se déplace de façon illimitée ou non sur cette grille dont le contour est considéré comme muni de cloisons extérieures, avec ou sans trous. Il s’agit, par exemple, de déterminer le nombre de points d'intersection touchés par un mobile ou la distance parcourue pour atteindre un point du parcours, pour revenir au point de départ ou encore pour s'immobiliser en un point donné ou dans un trou. Ces récréations peuvent être posées ou résolues sur du papier quadrillé. 

Le fou qui se déplace de façon continue sur un échiquier agit à la façon d'une bille de billard. Les problèmes de billard appartiennent à la classe des récréations topologiques.

2^e Diagramme qui permet de résoudre certaines récréations, notamment des questions de transvasement. Le diagramme correspond généralement à un parallélogramme délimité sur du papier triangulé. Le parallélogramme est  muni de coordonnées en abscisse et en ordonnée. Le chemin s'inspire du principe de déplacement de la bille au billard. 

Le diagramme ci-dessous montre de quelle façon on peut établir une mesure exacte de quatre litres à l'aide de trois récipients respectivement de trois, de cinq et de huit litres, ce dernier étant plein. Le point de départ est (0, 0) et le point d'arrivée est (4, 3).

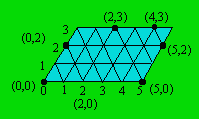
Les coordonnées de chaque point du diagramme indiquent les quantité de liquide pour les récipients de cinq et de trois litres, à mesure que les transvasements sont effectués. Le tableau suivant traduit les données du diagramme. À la fin, on remarque que le récipient de cinq litres en contient quatre.

© Charles-É. Jean

Index : B