Cavalier

° Parcours du cavalier. – Ensemble de cases visitées dans une grille par un cavalier selon son saut classique aux échecs. Le chemin du cavalier peut être fermé ou ouvert selon que la dernière cellule conduit ou non à la première. Il est fermé quand, dans un carré d’ordre n, le cavalier peut passer de la case n² à la case 1. Dans ce cas, on parle de circuit  du cavalier. 

Le chemin est ouvert quand le cavalier ne peut pas passer de la case n² à la case 1. Le chemin du cavalier peut être représenté par un graphe : c’est une ligne continue qui passe par le centre de chaque cellule. Cette ligne est constituée d’une séquence de segments reliant les cellules deux à deux. 

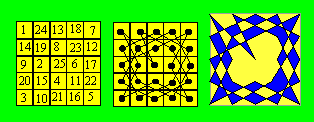
Voici le parcours d'un cavalier dans un carré d'ordre 5, marqué par les cases numérotées de 1 à 25, de même que le graphe et le motif correspondant :

Un mathématicien américain, L. D. Yarbrough, en 1968, a introduit le concept de chemin rentrant. Si le cavalier franchit la ligne continue au moins en un point, le chemin est rentrant. Si le cavalier s’arrête avant de franchir la ligne continue, on dit que le chemin est non rentrant. Le cavalier, sans couper son propre chemin, peut suivre le nombre maximum donné de segments dans une grille carrée d’ordre n où n est égal à 3 jusqu'à 12 lorsque le chemin est ouvert.

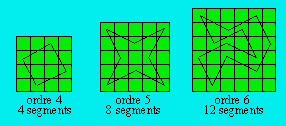
Voici des exemples de chemins dans des grilles d’ordres 3, 4, 5 et 6 :

Le cavalier, sans couper son propre chemin, peut suivre le nombre maximum donné de segments dans un carré d’ordre n où n est égal à 3 jusqu'à 12 lorsque le chemin est ouvert.

En 1823, H. C. Warnsdorff, un mathématicien allemand, a décrit une règle permettant de déterminer le chemin d’un cavalier qui se déplace dans une grille. 

On compte les cases possibles d’accès et on choisit la case qui en possède le plus petit nombre. On évite ainsi les cases desquelles le cavalier ne peut pas s’échapper. En conséquence, comme une case d’angle ne peut être atteinte qu’en passant par deux cases, si le cavalier atteint une de ces cases, il doit visiter la case d’angle et revenir par l’autre des deux cases. 

Une autre règle consiste à déplacer le cavalier en occupant d’abord les rangées périphériques toujours dans le même sens et à changer de sens au besoin. La règle des angles de Warnsdorff doit alors être appliquée. 

Voici quatre exemples de parcours du cavalier :
n Dans la grille ci-dessus, rendu à la case 64, le cavalier peut revenir au point 1. Le chemin est fermé.

n À partir du 1 dans le coin supérieur gauche, le cavalier se déplace d’un quadrant à l’autre dans le sens des aiguilles d’une montre. Rendu au saut 32, le cavalier avance dans le sens inverse toujours de 4 en 4.

n La figure suivante montre un carré d'ordre 9 dans lequel les 56 plus petits entiers consécutifs forment une couronne de deux rangées à la périphérie et les autres, jusqu'à 81, un carré d'ordre 5.

n À partir du 1 dans le coin supérieur droit, le cavalier se déplace dans l’enceinte extérieure formée par deux rangées à laquelle on ajoute deux cases de la troisième rangée horizontale. Rendu à 66, soit près des deux tiers du parcours, le cavalier entre dans l’enceinte intérieure et y termine sa course.

Les récréations consistent à trouver le meilleur chemin pour un cavalier. Dans certains cas, la règle exige que le déplacement soit effectué en un nombre minimal de coups ; dans d'autres cas, c'est la grille entière qu'il faut visiter et, parfois en revenant au point de départ. 

Historiquement, les premiers problèmes ont été posés sur l'échiquier. Toutefois, cette question peut être appliquée à des grilles carrées ou rectangulaires de mesures variées ou même à des grilles de différentes formes, comme la croix. On ne connaît pas de carré magique représentant le parcours du cavalier à l'intérieur d'une grille fermée. 

Le parcours du cavalier appartient à la classe des récréations combinatoires.

© Charles-É. Jean

Index : C

Voir : 

Cavalier d'Euler

Circuit du cavalier

Coins du cavalier

Échange de cavaliers