|
Cavalier
1e Pièce du jeu d'échecs qui avance obliquement,
dans tous les sens, du pâle au foncé ou du foncé au pâle, en sautant
toujours une case. Le déplacement a la forme d'un L. Le cavalier franchit une
case comme la tour et une case comme le fou. C'est la seule pièce des échecs
orthodoxes qui peut sauter par-dessus les autres. Elle est aussi la seule qui se
déplace de façon asymétrique.
Douze cavaliers adéquatement disposés sur
l'échiquier dominent ou occupent toutes les cases. Au maximum, 32 cavaliers
peuvent être placés de manière à ce qu'aucun ne soit pris par un autre. Le
nombre total de sauts possibles du cavalier sur un échiquier rectangulaire de pq
cases est égal à 2[(2p - 3)(2q - 3) -
1].
Le parcours
du cavalier dans une grille est
l'objet de nombreuses récréations. Le cavalier placé au centre en A peut
atteindre les cases marquées d'une étoile.
|
M
|
« |
M
|
« |
M
|
|
« |
M
|
|
M
|
« |
|
M
|
|
A |
|
M
|
|
« |
M
|
|
M
|
« |
|
M
|
« |
M
|
« |
M
|
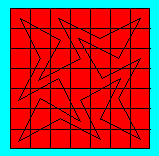
En 1968, L. D. Yarbrough, un mathématicien
américain, a donné un chemin fermé non rentrant
parcouru par le cavalier en 24 mouvements dans une grille 7 × 7.
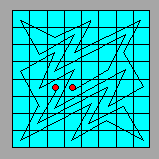
En 1930, le Britannique Thomas R. Dawson (1889-1951) a
trouvé un chemin ouvert non rentrant
parcouru par le cavalier en 35 mouvements dans une grille 8 × 8.
Le cavalier d'Euler, le
circuit du cavalier, le parcours
du cavalier et les coins du cavalier sont des exemples de récréation.
L'échange de cavaliers est un solitaire.
Le cavalier appartient à la classe des sauteurs.
2e Procédé de construction de carrés magiques
normaux d'ordre n où n est impair. On place d'abord le 1 dans
n'importe laquelle case. Par la suite, le déplacement se fait selon le saut du
cavalier toujours dans le même sens en choisissant pendant toute l'opération
l'une des quatre orientations suivantes : à droite et en haut, à droite et en
bas, à gauche et en haut, à gauche et en bas. Lorsqu'une case devant être
atteinte est en dehors du carré, le saut se fait sur la case extérieure
appropriée d'un carré élargi. Le nombre à inscrire est immédiatement
ramené dans le carré sur la même ligne ou la même colonne dans la position
correspondante selon le principe du cylindre. À la fin d'un cycle de n cases,
le nombre suivant est inscrit dans la case immédiatement inférieure de la
même colonne. Voici quatre carrés magiques d'ordre 5 formés selon ce
procédé :
|
1 |
14 |
22 |
10 |
18 |
|
18 |
1 |
14 |
22 |
10 |
|
10 |
18 |
1 |
14 |
22 |
|
12 |
25 |
8 |
16 |
4 |
|
7 |
20 |
3 |
11 |
24 |
|
24 |
7 |
20 |
3 |
11 |
|
11 |
24 |
7 |
20 |
3 |
|
18 |
1 |
14 |
22 |
10 |
|
13 |
21 |
9 |
17 |
5 |
|
5 |
13 |
21 |
9 |
17 |
|
17 |
5 |
13 |
21 |
9 |
|
24 |
7 |
20 |
3 |
11 |
|
19 |
2 |
15 |
23 |
6 |
|
6 |
19 |
2 |
15 |
23 |
|
23 |
6 |
19 |
2 |
15 |
|
5 |
13 |
21 |
9 |
17 |
|
25 |
8 |
16 |
4 |
12 |
|
12 |
25 |
8 |
16 |
4 |
|
4 |
12 |
25 |
8 |
16 |
|
6 |
19 |
2 |
15 |
23 |
Chacun des carrés permet la création d'un motif. Les voici
en regard de chaque carré :

© Charles-É. Jean
Index
: C
|
![]()
![]()