|
Complémentaires
°
Treillis magiques
complémentaires. – Deux treillis magiques normaux de même forme
et de même ordre sont complémentaires lorsque la somme des éléments
correspondants des deux treillis est égale à leur plus grand élément, augmenté
de l'unité.
L'application de cette notion permet la formation de treillis
magiques différents composés des mêmes éléments. La densité d'un carré
magique normal complémentaire est la même que celle du carré initial.
Toutefois, dans les autres treillis magiques, la densité peut être
différente.
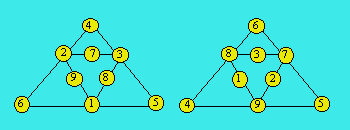
Les deux treillis suivants sont complémentaires. La densité du
premier est 12 et celle du deuxième est 18.
Deux carrés hétérogènes
formés des entiers de 1 à 9 sont complémentaires quand, pour toute rangée
correspondante, les sommes s1 et
s2 des éléments
des deux rangées sont égales à 30. Par exemple, si la somme d’une rangée
est 13, celle de la rangée correspondante sera 17.
Voici deux carrés
hétérogènes complémentaires l’un de l’autre :
|
|
|
|
6 |
|
|
|
|
24 |
|
4 |
6 |
3 |
13 |
|
6 |
4 |
7 |
17 |
|
7 |
2 |
9 |
18 |
|
3 |
8 |
1 |
12 |
|
1 |
8 |
5 |
14 |
|
9 |
2 |
5 |
16 |
|
12 |
16 |
17 |
11 |
|
18 |
14 |
13 |
19 |
Si on additionne les sommes des huit rangées, cette somme
est 107 dans le premier carré et 133 dans le second. Cette différence est due
à la position des éléments dans chaque carré.
© Charles-É. Jean
Index
: C
|
![]()
![]()