Circulaire

° Nombre circulaire. – Entier naturel qui, multiplié généralement par un entier, donne un résultat contenant les mêmes chiffres dans le même ordre, mais déplacés d’une position. On accepte un ou des zéros au début du nombre puisque ceux-ci sont aussi dans d’autres positions. Deux cas sont possibles.

L’unité du multiplicande devient le premier chiffre du produit. Par exemple, en multipliant 142 857 par 5, on obtient 714 285. Le 7 qui est l’unité du multiplicande est promu au premier rang du produit. Connaissant la période d’une fraction a/b, on peut trouver un nombre circulaire qui lui est associé en multipliant la période par le générateur de b. 

Le tableau suivant présente des fractions dont le dénominateur est 39, la période qui correspond à la fraction, le produit de la période et de 4 qui est le générateur de 39, puis la fraction associée à la seconde période. On y trouve donc neuf couples de nombres circulaires.

Connaissant la période d’une fraction a/b, on peut trouver une chaîne de nombres circulaires dont le premier maillon et le dernier coïncident. On calcule d’abord le générateur du dénominateur. On multiplie la fraction par le générateur. S’il y a lieu, on réduit la fraction de telle façon que le numérateur soit inférieur au dénominateur. Pour ce faire, on exprime la fraction en un nombre décimal ; on soustrait la partie entière et on multiplie par le dénominateur. Puis, on trouve la période qui correspond à cette dernière fraction. 

Dans le tableau suivant, on part de 1/41 et on passe par 37/41, 16/41, 18/41, 10/41. Les cinq périodes forment une chaîne de nombres circulaires.

Le premier chiffre du multiplicande devient l’unité du produit. Par exemple, en multipliant 142 857 par 3, on obtient 428 571. Le 1 qui est premier dans le multiplicande est déchu au dernier rang du produit. Connaissant la période d’une fraction a/b, on peut trouver un nombre circulaire qui lui est associé en multipliant la période par 10. 

Le tableau suivant présente des fractions dont le dénominateur est 17, la période correspondante à la fraction, le produit de la période et de 10 et la fraction associée à la période. Ce sont tous des couples de nombres circulaires.

Connaissant un nombre qui est la période d’une fraction a/b, on peut trouver une chaîne de nombres circulaires dont le premier maillon et le dernier coïncident. Dans le tableau suivant, on trouve la chaîne de nombres circulaires à partir de 1/73.

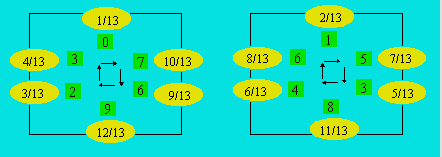
La fraction a/13, où a est un entier plus petit que 13, donne deux chaînes de nombres circulaires. Dans chacun des deux schémas suivants, on trouve six nombres circulaires. En lisant dans le sens horaire, on part d’une fraction et on note, dans l’ordre, les chiffres qui forment la période. Par exemple, la période de 1/13 est 076 923, celle de 12/13 est 923 076.

La théorie des nombres circulaires s'appuie sur le développement d'un nombre décimal périodique. Tout nombre cyclique est circulaire. Tout nombre circulaire n’est pas nécessairement cyclique. Par exemple, 153 846 qui est non cyclique est circulaire. Si on le multiple par 4, on obtient 615 384. 

On peut trouver des nombres circulaires par la multiplication à rebours.

© Charles-É. Jean

Index : C