° Critères de divisibilité. – Séquence d'opérations simples qui permettent de reconnaître si un entier est divisible par un autre sans qu’il soit nécessaire d’effectuer la division au long. Les règles permettant de reconnaître cette divisibilité sont identiques pour les divers systèmes de numération. Elles utilisent l’addition ou la soustraction.

Ö Par addition. Au nombre amputé de l’unité, on additionne le produit du générateur et de cette unité. On procède ainsi sur les résultats successifs jusqu'à ce qu’un nombre obtenu soit reconnu comme divisible ou non. Si ce nombre est divisible, le nombre initial l’est. Soit à vérifier si 24 365 est divisible par 13. Le générateur  de 13 est 4. On fait successivement : 2436 + (5 × 4) = 2456, 245 + (6 × 4) = 269, 26 + (9 × 4) = 62, 6 + (2 × 8) = 22. D’où, 24 365 n’est pas divisible par 13.

Ö Par soustraction. On calcule le complément du générateur. On procède comme pour l’addition. Soit à vérifier si 27 456 est divisible par 13. Le complément du générateur est 9. On fait successivement : 2 745 - (6 × 9) = 2691, 269 - (1 × 9) = 260, 26 - (0 × 9) = 26. Comme 26 est divisible par 13, alors 27 456 est divisible par 13.

Dans le tableau suivant, en regard de chaque diviseur, on peut lire des constantes. Vis-à-vis une constante sur la même ligne, on trouve un nombre de chiffres et une opération.

Pour vérifier la divisibilité, on choisit, dans la colonne du diviseur du tableau précédent, une constante qui semble la plus appropriée. Il s’agit alors d’amputer le dividende du nombre indiqué de chiffres en lisant de droite à gauche, de multiplier ce nouveau nombre par la constante et d’additionner (ou de soustraire) le produit du nombre amputé. On procède ainsi sur les résultats successifs jusqu'à ce qu’un nombre obtenu soit reconnu comme divisible ou non. 

Soit à diviser 2 535 409 par 43. On peut choisir la constante 4 dans la colonne de 43 : ce qui amène à amputer trois chiffres à la fois. On procède par des additions. On fait 2535 + (409 × 4) = 4171 et 4 + (171 × 4) = 688. Le nombre 688 est divisible par 43. D’où, 2 535 409 est divisible par 43. À un moment donné, si le dernier résultat contient un nombre de chiffres trop grand, on peut terminer la vérification en choisissant une autre constante obligeant à amputer moins de chiffres. De toute façon, tous les résultats ont le même caractère de divisibilité que le dividende initial.

Voici quelques façons de reconnaître si un nombre est divisible :
n Par 6. On additionne le dernier chiffre et quatre fois la somme des autres chiffres. Si la somme est divisible par 6, le nombre l’est aussi. Par exemple, 59 238 est divisible par 6 car 8 + 4(5 + 9 + 2 + 3) = 84 qui est divisible par 6.

n Par 7. a) On soustrait successivement le nombre formé par les trois derniers chiffres au nombre amputé de ces chiffres. Si le résultat est un multiple de 7, alors le nombre est divisible par 7. Pour vérifier si 458 274 579 est divisible par 7, on fait 458 274 - 579 = 457 695, 457 - 695 = - 238. Comme 238 est un multiple de 7, alors le nombre initial est divisible par 7. Tout nombre de six chiffres dont les deux tranches sont identiques est divisible par 7. Exemples : 8 008, 17 017, 235 235, 666 666. Tout nombre de neuf chiffres dont les trois tranches sont identiques est divisible par 7 si la tranche est divisible par 7. Par exemple 364 364 364 est divisible par 7 et 365 365 365 ne l’est pas.

n Par 7. b) On multiplie successivement le dernier chiffre par 2 et on soustrait le résultat du nombre amputé de son dernier chiffre. Si le résultat est un multiple de 7, alors le nombre est divisible par 7. Pour vérifier si 3171 est divisible par 7, on fait 317 - (1 × 2) = 315, 31 - (5 × 2) = 21. Comme 21 est un multiple de 7, alors 3171 est divisible par 7.

n Par 7. c) On sépare le nombre en tranches de deux chiffres à partir de la droite. On écrit sous chaque tranche le reste de la division par 7. On fait des tranches de trois chiffres avec ces résultats à partir de la droite. On fait la somme de chacune des trois colonnes. On écrit le reste de la division par 7 dans chaque colonne. On écrit le reste de la division par 7 du nombre formé par les deux premiers chiffres, puis le reste de la division par 7 du nombre formé par les deux derniers chiffres. Le nombre initial est divisible par 7 si les deux restes sont identiques. Le nombre 625 673 054 n’est pas divisible par 7. Voici un exemple :

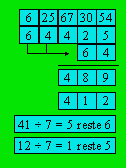
Cet algorithme a été créé par l’Américain L. Vosburgh Lyons.

n Par 7. d) On partage le nombre en deux tranches de trois chiffres à partir de la droite, la tranche de gauche pouvant avoir un, deux ou trois chiffres. On soustrait la plus petite tranche de l’autre. Si la différence est divisible par 7, le nombre l’est aussi. Par exemple, 834 750 est divisible par 7 car 834 - 750 = 84 qui est divisible par 7.

n Par 11. a) On soustrait successivement le dernier chiffre au nombre amputé de ce chiffre. Si le résultat est un multiple de 11, alors le nombre est divisible par 11. Pour vérifier si 6127 est divisible par 11, on fait 612 - 7 = 605, 60 - 5 = 55. Comme 55 est un multiple de 11, alors 6127 est divisible par 11. Tout nombre de six chiffres dont les deux tranches sont identiques est divisible par 11. Exemples. 8 008, 17 017, 235 235, 666 666.

n Par 11. b) On partage à partir de la droite le nombre en tranches de deux chiffres. On additionne les tranches. On fait la même opération jusqu'à ce qu’on reconnaisse un nombre divisible ou non par 11. Pour vérifier si 223 964 est divisible par 11, on fait 22 + 39 + 64 = 125, puis 1 + 25 = 26. Comme 26 n’est pas un multiple de 11, alors 223 964 n’est pas divisible par 11.

n Par 11. c) On soustrait successivement le nombre formé par les trois derniers chiffres au nombre amputé de ces chiffres. Si le résultat est un multiple de 11, alors le nombre est divisible par 11. Pour vérifier si 458 274 579 est divisible par 11, on fait 458 274 - 579 = 457 695, 457 - 695 = - 238. Comme 238 n’est pas un multiple de 11, alors le nombre initial n’est pas divisible par 11. Tout nombre de six chiffres dont les deux tranches sont identiques est divisible par 11. Exemples. 8 008, 17 017, 235 235, 666 666.

n Par 11. d) On partage le nombre en deux tranches de trois chiffres à partir de la droite, la tranche de gauche pouvant avoir un, deux ou trois chiffres. On soustrait la plus petite tranche de l’autre. Si la différence est divisible par 11, le nombre l’est aussi. Par exemple, 649 561 est divisible par 7 car 649 - 561 = 88 qui est divisible par 11.

n Par 11. e) On additionne les chiffres de rang impair, puis ceux de rang pair. Si la différence des deux sommes est 0 ou un multiple de 11, le nombre est divisible par 11. Par exemple, 82 753 est divisible par 11, car 8 + 7 + 3 = 18 et 2 + 5 = 7, puis 18 - 7 = 11. De même, 9 381 427 est divisible par 11, car 9 + 8 + 4 + 7 = 28 et 3 + 1 + 2 = 6, puis 28 - 6 = 22. Il résulte de cette règle que la divisibilité s’applique lorsqu’on échange des chiffres de même rang.

n Par 13. a) On multiplie successivement le dernier chiffre par 4 et on additionne le résultat au nombre amputé de son dernier chiffre. Si le résultat est un multiple de 13, alors le nombre est divisible par 13. Pour vérifier si 8541 est divisible par 13, on fait 854 + (1 × 4) = 858, 85 + (8 × 4) = 117, 11 + (7 × 4) = 39. Comme 39 est un multiple de 13, alors 8541 est divisible par 13.

n Par 13. b) On multiplie successivement les deux derniers chiffres par 3 et on additionne le résultat au nombre amputé de ses deux chiffres. Si le résultat est un multiple de 13, alors le nombre est divisible par 13. Pour vérifier si 281 970 est divisible par 13, on fait 2819 + (70 × 3) = 3029, 30 + (29 × 3) = 117. Comme 117 est un multiple de 13, alors 281 970 est divisible par 13.

n Par 13. c) On soustrait successivement le nombre formé par les trois derniers chiffres du nombre amputé de ces chiffres. Si le résultat est un multiple de 13, alors le nombre est divisible par 13. Pour vérifier si 458 274 579 est divisible par 13, on fait 458 274 - 579 = 457 695, 457 - 695 = - 238. Comme 238 n’est pas un multiple de 13, alors le nombre initial n’est pas divisible par 13. Tout nombre de six chiffres dont les deux tranches sont identiques est divisible par 13. Exemples. 8 008, 17 017, 235 235, 666 666.

n Par 13. d) On partage le nombre en deux tranches de trois chiffres à partir de la droite, la tranche de gauche pouvant avoir un, deux ou trois chiffres. On soustrait la plus petite tranche de l’autre. Si la différence est divisible par 13, le nombre l’est aussi. Par exemple, 327 470 est divisible par 13 car 470 - 327 = 143 qui est divisible par 13.

n Par 17. On multiplie successivement le dernier chiffre par 5 et on soustrait le résultat du nombre amputé de son dernier chiffre. Si le résultat est un multiple de 17, alors le nombre est divisible par 17. Pour vérifier si 78 013 est divisible par 17, on fait 7801 - (3 × 5) = 7786, 778 - (6 × 5) = 748, 74 - (8 × 5) = 34. Comme 34 est un multiple de 17, alors 78 013 est divisible par 17.

n Par 19. On additionne successivement le double du dernier chiffre et le nombre amputé de ce chiffre. Si le résultat est un multiple de 19, alors le nombre est divisible par 19. Pour vérifier si 108 132 est divisible par 19, on fait : 10 813 + (2 × 2) = 10 817, 1081 + (7 × 2) = 1095, 109 + (5 × 2) = 119, 11 + (9 × 2) = 29. Comme 29 n'est pas divisible par 19, alors 108 132 n’est pas divisible par 19.

n Par 23. On multiplie successivement le dernier chiffre par 7 et on additionne le résultat du nombre amputé de son dernier chiffre. Si le résultat est un multiple de 23, alors le nombre est divisible par 23. Pour vérifier si 84 733 est divisible par 23, on fait 8473 - (3 × 7) = 8452, 845 - (2 × 7) = 831, 83 - (1 × 7) = 76. Comme 76 n’est pas un multiple de 23, alors 84 733 n’est pas divisible par 23.

n Par 37. On partage le nombre en tranches de trois chiffres à partir de la droite, la tranche de gauche pouvant avoir un, deux ou trois chiffres. On additionne les tranches. Si la somme est divisible par 37, le nombre l’est aussi. Par exemple, 65 247 428 est divisible par 37 car 65 + 247 + 428 = 740 qui est divisible par 37.

n Par 7, 11 et 13. On partage le nombre en tranches de trois chiffres à partir de la droite, la tranche de gauche pouvant avoir un, deux ou trois chiffres. On additionne la première tranche de droite, la troisième, la cinquième, etc. On additionne la deuxième tranche de droite, la quatrième, la sixième, etc. On soustrait les deux sommes. Si la nouvelle somme est divisible par 1001 (7 × 11 × 13), le nombre est divisible par 7, 11 et 13. Pour vérifier si 8 241 446 070 est divisible par 7, 11 et 13, on fait 070 + 241 = 311, 446 + 8 = 454, 454 - 311 = 143. Comme 143 est un multiple de 11, de 13 et non de 7, alors 8 241 446 070 est divisible par 11, par 13 et non par 7.

n Par 3, 7 et 19. On multiplie successivement les deux derniers chiffres par 4 et on additionne le résultat du nombre amputé de son dernier chiffre. Si le résultat est un multiple de 399 (3 × 7 × 19), alors le nombre est divisible par 3, 7 et 9. Pour vérifier si 78 261 est divisible par 3, 7 et 19, on fait 782 + (61 × 4) = 1026, 10 + (26 × 4) = 114. Comme 114 est un multiple de 3, de 19 et non de 7, alors 78 261 est divisible par 3, par 19 et non par 7.

© Charles-É. Jean

Index : D