° Dissection géométrique. – Opération effectuée en deux temps : d'abord partage et découpage d'une figure géométrique ou d’un objet en un nombre fini de pièces, puis assemblage des pièces obtenues pour former une seconde figure, différente de la première. Cette opération peut se faire de diverses façons : d'une figure à une autre de forme différente, de plusieurs figures à une ou à des figures de formes déterminées, de plusieurs figures à une autre figure. 

Par exemple, deux carrés non congruents peuvent être découpés respectivement en deux et en trois pièces. Celles-ci peuvent être assemblées pour former successivement un parallélogramme, un rectangle et un carré, comme il est illustré.

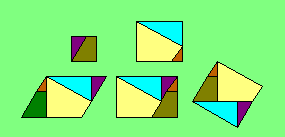
David Hilbert (1862-1943) a démontré que tout polygone peut être découpé pour former, par assemblage des pièces obtenues, tout autre polygone d'aire égale. Une solution élégante est celle où le découpage est fait en un nombre minimal de pièces. 

Il a été démontré que tout polyèdre ne peut pas être découpé de façon à former un autre polyèdre de même volume par assemblage des pièces obtenues. En particulier, aucun tétraèdre ne peut être découpé pour former un prisme. 

Les problèmes de dissection géométrique appartiennent à la classe des récréations de construction.

© Charles-É. Jean

Index : G