° Rectangle magique. – 1^e Treillis constitué d’une grille rectangulaire n ´ m dont les cases ou cellules contiennent des nombres disposés de telle manière qu’il existe une somme sur chaque ligne et une autre dans chaque colonne. Chaque somme est proportionnelle au nombre de cellules par rangée. Sous sa forme normale, un tel treillis reçoit les entiers de 1 à nm.  

Pour trouver les sommes par rangée, on fait la somme des entiers de 1 à nm ; on divise successivement par le nombre de lignes et le nombre de colonnes. Il n’existe pas de rectangle magique normal 2 ´ 3. 

Voici un rectangle normal 2 ´ 4 et un autre 2 ´ 6 :

Dans le premier rectangle, la somme sur chaque ligne est 18 et celle dans chaque colonne est 9, soit une moyenne de 4,5 par cellule. Dans le second rectangle, la somme sur chaque ligne est 39 et celle dans chaque colonne est 13, soit une moyenne de 6,5 par cellule. 

Le rectangle 3 ´ 4 ci-après est magique, mais il n’est pas normal. La somme est 28 sur chaque ligne et 21 dans chaque colonne. Le rectangle 3 ´ 5 est magique et normal. La somme sur chaque ligne est 40 et dans chaque colonne 24, soit une moyenne de 8.

Le rectangle 4 × 6 suivant contient les nombres de 1 à 24. La somme des nombres est 75 horizontalement et 50 verticalement, soit une moyenne de 12,5 par cellule.

Pour qu'un rectangle magique normal de cette classe existe, il faut que la somme de ses éléments soit divisible par le nombre de rangées horizontales et par le nombre de rangées verticales. 

Le rectangle magique ci-après contient des cases noires ou égales à 0. On doit écrire chacun des nombres de 2 à 9 pour que la somme soit 18 dans chaque rangée horizontale de quatre cases et dans chaque rangée verticale de trois cases. Les nombres 1 et 10 sont en bonne position. La solution est donnée.

2^e Treillis constitué de carrés accolés qui forment un rectangle. Des nombres sont distribués au sommet des carrés tels que leur somme appelée densité est la même sur chaque carré. Le plus petit rectangle magique comprend deux carrés qui supportent quatre cellules chacun dont deux sont communes. 

Dans sa forme normale, il contient les nombres consécutifs de 1 à 6. Il existe cinq densités D : 12, 13, 14, 15 et 16. Selon la classification proposée dans l’article Treillis magiques, ce rectangle peut être codé 6-4-2-24-1a. Voici cinq configurations dont une par densité :

On peut insérer une cellule au centre de la jonction des deux carrés et y disposer les nombres de 1 à 7. Les densités possibles varient de 17 à 23. Voici quatre configurations :

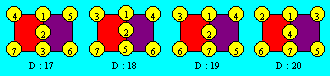
Les configurations pour les autres densités peuvent être obtenues en soustrayant chaque élément de 8. La configuration de gauche ci-après est formée de trois carrés accolés. La densité est 18. Celle de droite est formée de quatre carrés. La densité est 21.

Dans le premier treillis, la somme est aussi 18 dans chaque rangée horizontale de quatre cellules.