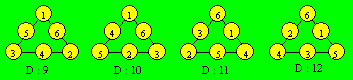
Les densités 9 et 12 sont complémentaires par rapport à 21, de même que les densités 10 et 11. Le triangle de grandeur suivante reçoit quatre cellules sur chaque côté. Il est formé de neuf cellules. Dans sa forme normale, il contient les nombres consécutifs de 1 à 9. Il existe cinq densités : 17, 19, 20, 21 et 23. Ce treillis peut être codé 9-4-3-36-1a. Voici une configuration pour chaque densité :

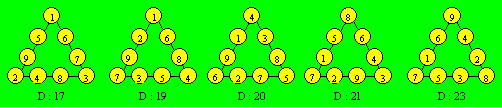
La somme des densités complémentaires est 40. Comme il n’existe pas de densité 18, il n’existe pas de densité 22. Le triangle de grandeur suivante reçoit cinq cellules sur chaque côté. Il est formé de 12 cellules. Dans sa forme normale, il contient les nombres consécutifs de 1 à 12. Il existe 10 densités, soit de 28 à 37. Son code est 12-5-3-39-1a. Voici une configuration pour chacune des densités de 28 à 32 :

La somme des densités complémentaires est 65. Une configuration pour chacune des autres densités peut être trouvée en soustrayant chaque élément de 13. Soit n le nombre de cellules par côté, la plus petite densité pour chaque valeur de n est (3n² - 5n + 6)/2 et la plus grande est (3n² + n - 6)/2.

2^e Treillis formé d’un triangle partagé en trois triangles sur les côtés desquels les nombres sont placés de telle manière que leur somme appelée densité est identique sur chacun des trois triangles. Le plus petit triangle magique reçoit six cases ou cellules sur chaque côté. Il est formé de 10 cellules. Dans sa forme normale, il contient les nombres consécutifs de 1 à 10. Il existe 11 densités D, soit de 28 à 38. Ce triangle peut être codé 10-6-3-406-1a. 

Voici une configuration pour chaque densité de 28 à 32 :

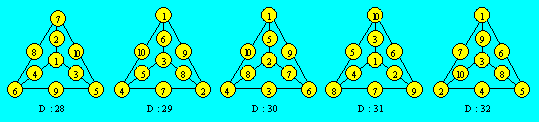
La somme des densités complémentaires est 66.

3^e Treillis formé d’un grand triangle dont les médianes produisent un triangle intérieur. Le treillis comprend six rangées : les trois côtés du grand triangle et les trois du triangle intérieur. Les nombres sont distribués de telle manière que leur somme appelée densité est identique dans chacune des six rangées de trois cellules. Dans sa forme normale, le treillis contient les nombres consécutifs de 1 à 9. Il existe quatre densités D : 12, 14, 16 et 18. Ce triangle peut être codé 9-3-6-333-1a. 

Voici une configuration pour chaque densité :

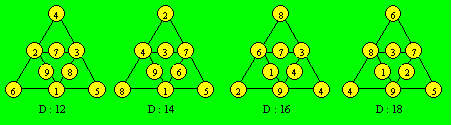
La somme des densités complémentaires est 30. Dans la première et la quatrième configuration, on pourrait ajouter une rangée, soit la médiatrice qui joint le sommet.

4^e Treillis formé d’un triangle constitué par cinq rangées : les côtés du triangle, la médiatrice qui touche au sommet et une médiane posée horizontalement. Les nombres sont distribués de telle manière que leur somme appelée densité est identique dans chacune des cinq rangées de trois cellules. Dans sa forme normale, le treillis contient les nombres consécutifs de 1 à 7. Il existe une seule densité, soit 12. Ce triangle peut être codé 7-3-5-160-1a. Voici deux configurations :

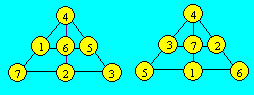
La deuxième configuration peut être obtenue de la première par rotation et par symétrie. L’élément du sommet est toujours le tiers de la densité.