Solutions 1 à 20
1. Banc d’Élise

Assise sur un banc dans un parc, Élise a préparé une grille 5 × 5. Elle peut y compter quatre carrés 4 × 4 qui peuvent coïncider.

Dans cette grille, combien peut-on compter de carrés 2 × 2 qui peuvent coïncider ?

2. Crayon de Louis

Louis a tracé la figure ci-après. Il demande à Louise de tracer cette figure sans lever le crayon et sans passer deux fois sur une même ligne. Il lui est permis au besoin de passer plus d’une fois sur un même point d’intersection.

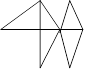
De quel point Louise doit-elle partir pour tracer cette figure ?

3. Ballons de Lise

Lise a disposé neuf ballons dans les cases colorées d’un losange comme ci-après. Chaque côté du losange contient trois ballons. Lise pourrait placer cinq ballons à l’intérieur de la bordure pour avoir un losange plein.

Combien Lise pourrait-elle placer de ballons à l’intérieur de la bordure d’un losange qui contiendrait cinq ballons par côté et avoir ainsi un losange plein ?

4. Cure-dents de Maxime

Maxime a dessiné les sept hexagones suivants.

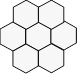
Combien Maxime devra-t-il utiliser de cure-dents pour reproduire cette figure ?

5. Chemins d’un minou

Un minou part du point du coin supérieur gauche et veut se rendre au point du coin opposé. Il se déplace de gauche à droite et de haut en bas en suivant les lignes.

Combien y a-t-il de chemins possibles ?

6. Dominos de Sofia

Sofia dépose des dominos dans une grille 5 ´ 5 dont les quatre cases des coins ont été coupées. Un domino occupe deux cases.

Combien Sofia peut-elle placer de dominos ?

7. Triangles de Manuel

Manuel a tracé la figure suivante qui est composée de petits triangles.

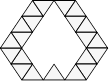
Combien manque-t-il de petits triangles à l’intérieur de cette figure ?

8. Kevin accole

Kevin dessine cinq petits carrés de même grandeur. Il les accole comme ci-dessous. Il peut ainsi compter 12 segments unitaires sur les côtés de la figure obtenue.

Assemblez cinq petits carrés de façon à compter 10 segments unitaires sur les côtés de la nouvelle figure.     

9. Triangles de Yolande

Yolande a dessiné un triangle équilatéral. Elle a tracé comme ci-après deux parallèles à la base et trois perpendiculaires à cette même base.

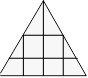
À l’exception du grand triangle, combien peut-on compter de triangles de toute grandeur dans cette figure ?

10. Comme les abeilles

Marcel trace un hexagone régulier. Il dit à Marcelle, sa jumelle : « Pourrais-tu, dans cette figure, tracer trois hexagones de même grandeur et trois losanges de même grandeur ? Je te donne un indice. Les losanges touchent au contour de la figure. »

Partagez l’hexagone en six parties.

11. Tarte de Louis

Louis connaît la façon classique de partager une tarte en quatre parties de même forme et de même grandeur. Il s’agit de tracer deux droites perpendiculaires qui passent par le centre.

Trouvez une autre façon de partager une tarte en quatre parties de même forme et de même grandeur.

12. Châteaux de Ludovic

Ludovic a dessiné ces 15 châteaux. En passant par au moins quatre châteaux, il a tracé tous les carrés de toute grandeur.

Combien Ludovic a-t-il pu tracer de carrés ?

13. Bâtonnets de Doris

Doris prend 18 bâtonnets et forme la grille ci-après. Il obtient ainsi six petits carrés.

Enlevez trois bâtonnets pour obtenir quatre carrés.

14. Chemin royal

Le roi de trèfle se trouve dans la pièce en haut à droite. Il veut retrouver la dame de trèfle qui est dans le coin opposé. Pour ce faire, il doit passer par toutes les portes une seule fois chacune.

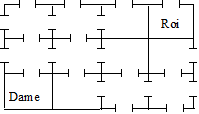
Trouvez un chemin que le roi devra parcourir.

15. Balles de tennis

Renée dispose huit balles de tennis en un carré comme ceci.

Déplacez une balle pour former trois carrés.

16. Chat à l’affût

Un chat est placé en C. Il surveille une souris placée en S. Pour attraper la souris, le chat doit emprunter l’un des chemins en se déplaçant de gauche à droite et sans jamais revenir en arrière. Dans sa tête, le chat se dit : « S’il y a plus de 12 chemins possibles, je vais perdre le nord. »

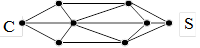
Le chat finira-t-il par attraper la souris ou plutôt perdra-t-il le nord ?

17. Croix de Julie

Julie prend six jetons et les dispose en croix comme ci-après. On compte trois jetons dans la rangée horizontale et quatre dans la rangée verticale.

Déplacez un jeton pour avoir deux rangées de quatre jetons.

18. Carré de François

François trace un carré dans lequel il forme des carrés et un rectangle.

Outre le grand carré, combien y a-t-il de carrés de toute grandeur dans cette figure ?

19. Cerises d’Émerise

Émerise vient de terminer de planter des cerisiers dans un terrain carré. On y trouve cinq cerisiers sur chacun des côtés du carré et cinq cerisiers sur chacune des diagonales.

Combien Émerise a-t-elle planté de cerisiers au minimum ?

20. Boutons de Narcisse

Narcisse prend six boutons et les dispose comme ci-après. Il a réussi trois rangées de trois boutons chacune.

Disposez les six boutons en quatre rangées de trois boutons chacune.

                                                                                                                         Solutions 21 à 40

21. Points de Laura

Laura a disposé 18 points comme ci-après. En partant de n’importe lequel point, elle joint ceux-ci sans lever le crayon et sans passer deux fois sur un même trait.

Combien Laura peut-elle construire de rectangles au maximum ?

22. Bricolage de Flavie

Flavie sort son matériel de bricolage. Elle découpe sept jetons ; puis elle forme un triangle avec six jetons. Cela donne trois rangées de trois jetons chacune.

Ajoutez le septième jeton permettant de former six rangées de trois jetons chacune.

23. Propos au parc

Assise sur un banc, Charlotte écoute des propos des gens qui passent. En même temps, elle dessine la figure suivante dans laquelle on compte 13 petits carrés.

À l’exception des petits carrés, combien y a-t-il de carrés de toute grandeur dans cette figure ?

24. Distraction d’abeille

Une abeille distraite avance sur le contour des alvéoles de la figure ci-après en partant du point supérieur jusqu'au point inférieur donné. Le contour de chaque alvéole mesure 30 centimètres. L'abeille emprunte le chemin le plus long sans passer plus d'une fois sur un même côté et sans toucher le point inférieur deux fois.

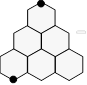
Quelle distance l'abeille devra-t-elle parcourir ?

25. Découpure de Tristan

Tristan a tracé une grille 4 × 4 et y a découpé un carré dans le coin inférieur gauche.

Partagez cette figure tronquée en quatre parties de même forme et de même grandeur.

26. Rectangles de Catherine

Catherine a dessiné la figure suivante qui comprend sept rectangles formés d’une seule pièce.

À part les rectangles formés d’une seule pièce, combien peut-on compter de rectangles de toute grandeur ?

27. Au golf

Roger distribue des balles de golf comme ci-après. Il veut obtenir une autre disposition telle que la figure est renversée de bas en haut.

Déplacez un minimum de trois balles pour obtenir la figure désirée.

28. Fleurs de Yasmin

Yasmin adore les roses de toutes couleurs. Il en distribue sur la bordure d’un pentagone régulier. Il en plante six sur chaque côté.

Combien Yasmin plantera-t-il de roses au minimum ?

29. Rectangle de Marcelle

Marcelle a dessiné le rectangle ci-après. Elle y a tracé deux diagonales et un segment vertical.

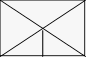
Combien y a-t-il de triangles de toute grandeur dans cette figure ?

30. Dans l’œil

Laurie a découpé des petits triangles et les a assemblés pour former la figure ci-après. Elle a laissé une partie vide à l’intérieur.

Combien devrait-il y avoir de petits triangles dans la partie vide de cette figure ?

31. Jetons d’Alicia

Alicia a disposé quatre jetons comme ci-après. Elle forme ainsi une seule rangée de trois jetons.

Ajoutez quatre jetons pour avoir cinq rangées de trois jetons chacune.

32. Hexagones de Denise

Denise a dessiné des triangles dans cet hexagone. En suivant les lignes, elle repère d’autres hexagones.

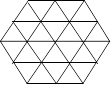
À l’exception du grand hexagone, combien peut-on compter d’hexagones dans cette figure ?

33. Chocolat de Luc

Luc a acheté une barre de chocolats comportant 24 morceaux identiques. Les chocolats sont disposés en un rectangle 4 × 6 comme ceci.

Combien peut-on compter de carrés 2 × 2 ?

34. Jetons d’Élodie

Élodie fait deux piles de jetons de même grandeur. Dans l’une des piles, l’épaisseur des jetons est de 3 centimètres ; dans l’autre, elle est de 4 centimètres. Elle veut faire une pile de 19 jetons dont la hauteur est de 65 centimètres.

Combien Élodie devra-t-elle prendre de jetons dans chacune des deux piles ?

35. Carrés de Françoise

Françoise a dessiné 10 petits carrés et les a assemblés comme suit. Elle dit à sa sœur Mira : « En partant d’un point d’un sommet et en suivant les lignes de façon continue, construis le plus grand nombre de petits carrés. »

Combien Mira pourra-t-elle construire de petits carrés au maximum ?

36. Triangles de Manuel

Manuel a tracé la figure ci-après. Il a compté tous les triangles composés d’une ou de plusieurs parties.

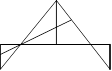
Combien peut-on compter de triangles dans cette figure ?

37. Figure de Béatrice

Béatrice a découpé 16 petits carrés et les a assemblés comme ceci.

Partagez cette figure en quatre parties de même forme et de même grandeur.

38. Carton de Philippe

Sur du carton, Philippe trace deux carrés de même grandeur. Il trace une diagonale dans chaque carré et découpe les pièces.

Assemblez les quatre pièces de façon qu’on puisse voir deux carrés qui ne sont pas accolés.

39. D’une étoile à l’autre

Livia part d’une étoile. En joignant les étoiles sans lever le crayon et sans passer deux fois sur un même segment, elle trace des petits carrés. Un petit carré réussi vaut 1 point ; chaque carré non fermé vaut 1/4 point.

Quel est le plus grand nombre de points que Livia peut obtenir ?

40. Carrés de Francis

Francis dessine la figure ci-après qui est composée de 20 triangles isocèles. Il compte alors quatre carrés entre les deux parallèles. Sur le même modèle, sa sœur dessine une figure composée de 60 triangles isocèles.

Combien la figure de la sœur de Francis comportera-t-elle de carrés entre les deux parallèles ?

                                                                                                                    Solutions 41 à 60
41. Carrés de Rita

Rita a dessiné la figure ci-après qui est composée de 16 petits carrés.

À l’exception des petits carrés, combien peut-on compter de carrés de toute grandeur dans cette grille ?

42. Perles de Tom

Tom pose une perle noire, celle du haut à droite. Il enfile d’autres perles d’abord vers la gauche, puis en suivant le chemin indiqué.

Combien de perles Tom devra-t-il ajouter pour se rendre jusqu’à la perle noire du bas ?

43. Partage d’Ursule

Ursule a trouvé six façons de partager une grille 4 ´ 4 en deux parties telles que les deux parties peuvent être superposées. Voici trois façons :

Trouvez au moins une autre façon de partager la grille.

44. Au ping-pong

Gabriel a disposé sept balles de ping-pong comme ci-après. Il a obtenu trois rangées de trois balles chacune.

Déplacez une balle pour avoir quatre rangées de trois balles chacune.

45. Frénésie de bijoux

Le comte Grand-Œil dépose 12 diamants comme ci-après sur le bureau de la comtesse. Celle-ci peut ainsi former six petits carrés distincts ayant un diamant à chaque sommet. Il dit à la comtesse : « Je te donne les diamants que tu enlèveras à la condition de laisser un seul carré. »

Combien la comtesse peut-elle gagner de diamants au minimum ?

46. Triangles d’Élodie

Élodie a tracé la figure ci-après. Elle y compte neuf triangles formés d’une seule partie.

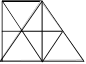
Combien y a-t-il triangles formés de plus d’une partie ?

47. Citrons de Réal

Réal a placé 18 citrons en un rectangle comme ci-après. Il s’amuse à tracer des rectangles qui passent par six citrons voisins.

Combien Réal pourra-t-il tracer de rectangles ?

48. Potager d’Amélie

Amélie a partagé son potager en 12 petits carreaux comme ci-dessous.

Partagez le potager en quatre parties de même forme et de même grandeur.

49. Allumettes de Biche

Biche prend 13 allumettes et les dispose sur la grille ci-après. Elle forme ainsi quatre carrés. Elle décide d’ajouter 20 allumettes à la droite selon le même modèle.

Combien de carrés additionnels pourront être formés ?

50. Grille de Mathias

Mathias a tracé une grille 3 × 5 au centre de laquelle il a noirci un petit carré.

Combien y a-t-il de rectangles 2 × 3 qui contiennent la case noire ?

51. Rectangle de Francis

Francis a dessiné une grille rectangulaire 5 × 7. Il a coloré les cases de la bordure. On peut compter 15 cases à l’intérieur de celle-ci.

De son côté, Francine trace une grille rectangulaire 8 × 10. Combien pourra-t-elle compter de cases à l’intérieur de la bordure ?

52. Grille d’Alexis

Alexis a préparé une grille 5 × 5. Il s’amuse à compter les carrés de toute grandeur.

À l’exception du grand carré et des petits carrés, combien y a-t-il de carrés de toute grandeur dans cette grille ?

53. Cadran de Béatrice

Béatrice a dessiné un cadran. Elle veut partager le cadran en quatre parties. Les sommes des nombres de chacune des parties doivent être des nombres consécutifs.

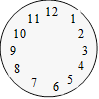
Faites un partage.

54. Quadrillé de Carol

Sur du papier quadrillé, Carol a tracé cette figure qui est composée de 16 petits carrés.

Partagez cette figure en quatre parties de même forme et de même grandeur.

55. Allumettes de Juliane

Juliane prend 12 allumettes et forme la grille ci-après. Elle obtient ainsi quatre petits carrés. Elle veut élargir la figure vers la droite.

 Combien d’allumettes faudrait-il ajouter pour former un rectangle constitué de 12 petits carrés ?

56. Tuiles de Cédric

Cédric accole quatre tuiles comme ci-après. Il compte 10 segments unitaires sur les côtés de la figure obtenue.

Assemblez cinq tuiles de façon à compter 13 segments unitaires sur les côtés de la figure.

57. Échiquier de Théo

Théo sort son échiquier. Il recouvre une partie avec un carton rectangulaire de couleur.  

Combien de cases noires sont cachées sous le carton ?

58. Les T de Tibère

Tibère trace deux T dans la grille 5 × 7 ci-après. Il veut placer d’autres T de même taille.

Disposez d’autres T dans la grille pour que la grille soit remplie le plus possible.

59. À deux vitesses

Isabelle a tracé un sentier autour de 18 tuiles qui sont représentées ci-après. Deux mouches partent en même temps du point N qui est l’intersection des deux côtés du petit carré. Elles marchent toutes deux sur le contour de la figure. La mouche A part vers la gauche et la B, vers le bas. Pendant que la mouche A parcourt un côté d’une tuile, la mouche B parcourt deux côtés.

À quel endroit les deux mouches se rencontreront-elles ?

60. Réseaux de Zénon

Zénon a dessiné les trois réseaux ci-après. Il tente de tracer chacun des réseaux en passant par toutes les lignes une seule fois et sans lever le crayon.

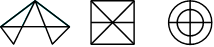
Combien de réseaux peuvent-ils être parcourus d’un seul trait ?

                                                                                                                         Lire la suite