Récréation 1
Lors d’une fête pour souligner le jour du Travail chez les léporidés, 12 lapins se réunissent dans un clapier. À leur arrivée, tous les lapins se donnent une poignée de pattes.

Combien de poignées de pattes ont été données ?

Récréation 2
Ruth prépare neuf petits cartons sur lesquels elle écrit les nombres impairs de 1 à 17. Elle veut placer ces cartons dans une grille 3 ´ 3. La somme des nombres dans chaque ligne, colonne et diagonale doit être la même. Le jeton 17 est en bonne position.

Distribuez les petits cartons dans la grille.

Récréation 3
Charlotte dessine cette figure.

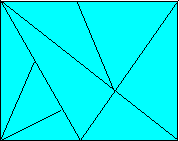
Combien de triangles de toute grandeur peut-on compter dans cette figure ?

Récréation 4
Jérémie a placé des boules rouges et des boules bleues en un triangle comme ci-après. Chaque rangée horizontale débute par une boule rouge ; puis il y a alternance entre les couleurs.

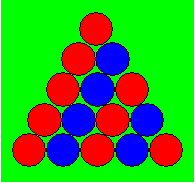
Combien de boules bleues seront nécessaires pour former un triangle ayant 20 boules à la base ?

Récréation 5
Ovide a trois récipients qui peuvent contenir trois, sept et neuf litres d’eau. Le récipient de neuf litres est plein. Les deux autres sont vides.

Comment peut-on s’y prendre pour avoir une mesure de cinq litres ?

Récréation 6
Un lièvre se déplace en ligne droite. Il avance de cinq kilomètres une journée et le lendemain il revient sur ses pas en parcourant deux kilomètres. Il continue de se déplacer selon le même rythme dans les jours qui suivent.

Combien de kilomètres aura parcouru ce lièvre quand il sera à 23 kilomètres de son point de départ ?

Récréation 7
Sara dessine neuf étoiles dans un carré 3 ´ 3 comme ci-après. En passant par trois ou quatre étoiles, elle trace des triangles. Voici un exemple en passant par quatre étoiles :

Combien peut-on tracer de triangles rectangles différents en passant par trois ou quatre étoiles ?

Récréation 8
Sébastien prend le calendrier d’une année bissextile. Le 1^er janvier est un dimanche.

Combien y a-t-il de vendredis 13 en cette année bissextile ?

Récréation 9
Pauline prend huit jetons et les numérote de 2 à 10, sauf 9. Elle veut disposer les jetons sur la figure ci-après. La somme doit être 15 dans chaque rangée de deux ou de trois jetons reliés par une droite.

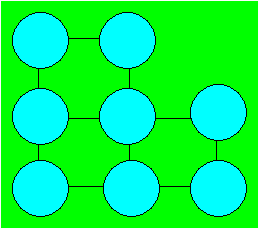
Trouvez une façon de distribuer les jetons.

Récréation 10
Phonsine dessine une grille 3 × 3. Elle découpe huit jetons. Sur chaque jeton, elle écrit les lettres de BON ET CON ; puis elle dépose chaque jeton sur la lettre correspondante dans cette grille.

Elle doit déplacer les jetons un à un sur toute case libre en les glissant sur une case voisine ou en sautant au-dessus d’une case, toujours horizontalement ou verticalement. À la fin, elle doit obtenir cette grille.

Exécutez cette tâche en effectuant le moins possible de mouvements.

Récréation 11
Quatre amis : Luc, Sam, Tom et Yan ont décidé de miser un certain montant d’argent à un jeu de hasard. À chaque partie, le perdant donne à chacun des trois autres la moitié du montant que chacun possède. Après quatre parties, chaque joueur possède 81 louis. Les perdants ont été dans l’ordre : Sam, Tom, Luc et Yan.

Combien de louis chacun avait-il au début ?

Récréation 12
Bianca a écrit les chiffres de 0 à 9 avec des cure-dents comme ci-après. Elle veut connaître des couples de nombres dont la somme est 65 et qui utilisent 21 cure-dents pour leur écriture.

Combien y a-t-il de tels couples ?

Récréation 13
Guillaume a découpé six triangles équilatéraux. En les assemblant, il a trouvé 12 configurations différentes. En voici une :

Trouvez au moins cinq autres configurations.

Récréation 14
Dans sa fermette, Justine possède 100 lapins. Elle voit naître sept lapins aux jours 1, 3, 5, 7, 9, etc. Les jours où il n’y a pas de naissance, trois lapins disparaissent dans la nature.

Combien de jours seront nécessaires pour qu’il y ait 200 lapins dans la fermette de Justine ?

Récréation 15
Henri prépare 12 jetons et les numérote de 1 à 12. Il désire placer les 12 jetons de façon à réaliser quatre additions comme ci-dessous.

Trouvez au moins une disposition possible.

Récréation 16
Sabin a disposé ses 34 chevaux de collection dans trois boîtes.
S’il retire un cheval de la boîte A, celle-ci en contient deux fois plus que la B.
S’il retire un cheval de la boîte B, celle-ci en contient deux fois moins que la C.

Combien Sabin a-t-il disposé de chevaux dans chaque boîte ?

Récréation 17
Flavie dessine une grille 3 ´ 3 avec des allumettes.

Combien d’allumettes seront nécessaires pour dessiner une grille 10 ´ 10 ?

Récréation 18
Samuel prend un cavalier et le place dans le coin supérieur droit d’une grille carrée 5 ´ 5. Le cavalier se déplace en L comme aux échecs. Au deuxième mouvement, le cavalier atteint la case 2 et au troisième mouvement la case 3.

Continuez à déplacer le cavalier pour qu’il visite au moins 24 cases, chacune une seule fois. Numérotez les cases au passage.

Récréation 19
Emma dessine le pentagone ci-après. Elle veut placer chacun des nombres de 1 à 10 pour que la somme soit la même sur chacun des côtés du pentagone.

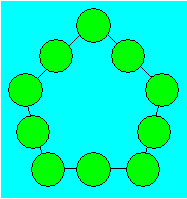
Distribuez les nombres sur ce pentagone pour que cette somme soit la plus petite possible.

Récréation 20
Sylvie prend sa calculatrice et multiplie les nombres consécutifs. Par exemple, elle écrit :

Sylvie décide de multiplier les 50 nombres consécutifs à partir de 6. 

Combien y aura-t-il de zéros à la fin du produit ?

Récréation 21
Léon et William ont inventé un jeu de billes. À tour de rôle, chacun dépose au choix trois, quatre ou cinq billes dans une boîte commune. Le gagnant est celui qui, après un dépôt, fait en sorte que la boîte contienne exactement 45 billes.

Quelle stratégie Léon devra-t-il appliquer s’il veut toujours gagner, en admettant que William joue sans plan précis ?

Récréation 22
Julien trace un cercle. Il y dessine 15 points. Puis, il relie les points chacun à chacun par un trait.

Combien de traits Julien devra-t-il tracer ?

Récréation 23
Zacharie a dessiné la figure suivante.

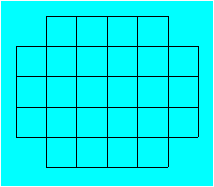
Combien de carrés de toute grandeur peut-on compter dans cette figure ?

Récréation 24
Thomas a dessiné la figure ci-après. Il veut colorier les cercles de telle manière que deux cercles voisins reliés par une droite sont de teinte différente.

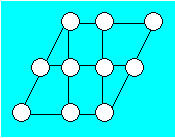
Au minimum, combien de couleurs seront nécessaires ?

Récréation 25
Une mouche part du point A et s’arrête au point B. Elle circule uniquement de gauche à droite et de bas en haut.

Combien de chemins différents la mouche peut-elle parcourir ?

Récréation 26
Deux araignées se déplacent à la même vitesse. L’araignée Atricus part cinq minutes avant la Salticus et elle avance de quatre pas à la minute. L’araignée Salticus se déplace de sept pas à la minute. Elles arrivent en même temps devant un acacia.

Combien de temps sera nécessaire à l’araignée Salticus pour rejoindre l’autre devant l’acacia ?

Récréation 27
Magalie dessine des croix qui sont formés de cinq petits carrés. Elle désire colorier chaque croix avec exactement quatre couleurs. Chaque croix doit avoir un coloriage différent. Par exemple, les deux croix ci-après sont considérées comme équivalentes en couleurs.

Combien Magalie pourra-t-elle colorier de croix différentes ?

Récréation 28
Olivier prépare neuf petits cartons sur lesquels il écrit les nombres de 1 à 9. Dans la grille 3 ´ 3, il veut placer les cartons de telle manière que chaque nombre de droite est supérieur à son voisin de gauche et que chaque nombre du haut est inférieur à son voisin du bas. Olivier a rempli cette grille ainsi.

Trouvez d’autres façons de remplir la grille.

Récréation 29
Florence prépare six jetons sur lesquels elle écrit les nombres de 2 à 7. Elle doit placer les jetons dans le tableau ci-après. Dans un premier essai, elle a disposé les jetons de telle manière que la somme est 801.

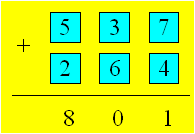
À l’exception de 801, combien de sommes différentes peut-on trouver ?

Récréation 30
Alice a écrit RÉCRÉOMATH sous forme d’une addition. Chaque lettre représente un chiffre différent de 0 à 9. Alice a trouvé cette égalité : 674 + 678 = 1352. Il existe en tout 66 possibilités.

Trouvez au moins une autre possibilité.

Récréation 31
Carole dessine et découpe les jetons numérotés : 3, 4, 5, 8, 9, 10. Elle doit placer chacun des jetons dans les cases vides de la grille ci-après. La somme des nombres de chaque rangée horizontale, verticale et diagonale doit être 27. Deux nombres sont en bonne position.

Complétez la grille.

Récréation 32
Dans cette figure, Rosalie a écrit les lettres de son prénom. On peut le lire en reliant les lettres voisines obliquement

Combien y a-t-il de façons de lire ROSALIE ?

Récréation 33
Juliette décore une salle d’accueil. Au plafond et sur deux murs, elle place deux crochets. Puis, elle joint les crochets avec des guirlandes. Elle a alors besoin de 12 guirlandes comme il est illustré.

Dans une autre salle, Juliette place six crochets au plafond et quatre sur chacun des deux murs.

Combien Juliette aura-t-elle besoin de guirlandes ?

Récréation 34
Laurence a représenté les cinq premières lettres comme ci-après. Elle poursuit l’écriture des autres lettres selon la même régularité.

A = °

B = ° °

C = ° ° °

D = ° ° ° °

E = ° ° ° ° °

Trouvez des mots qu’on peut écrire en utilisant 60 fois le symbole °.

Récréation 35
Maélie prend neuf boules et les numérote de 1 à 9. Elle désire placer les boules pour que la somme de chaque rangée de deux, de trois ou de quatre boules reliées par une droite soit 14.

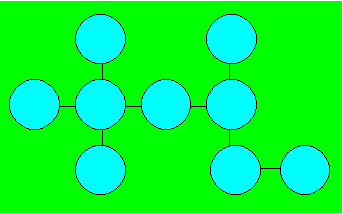
Distribuez les boules.

Récréation 36
Avec 1, 2, 3 et 4, Nathan forme des groupes de deux nombres différents dont la somme est 5. Il a trouvé deux groupes : 1 + 4 = 5 et 2 + 3 = 5. Il s’intéresse maintenant aux nombres de 1 à 12.

Avec les nombres de 1 à 12, combien peut-on former de groupes de trois nombres différents dont la somme est 20 ?

Récréation 37
Jacob a tracé la grille rectangulaire 3 ´ 4 ci-après. Il y dénombre sept rectangles 2 ´ 3.

Combien Jacob peut-il compter de rectangles 2 ´ 3 dans une grille rectangulaire 8 ´ 9 ?

Récréation 38
Nadia découpe quatre triangles rectangles isocèles de même grandeur. Elle les assemble successivement côté par côté de façon à former ces deux configurations.

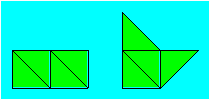
Il existe six autres configurations différentes. Trouvez-en au moins trois.

Récréation 39
Gabriel a écrit les nombres de 1 à 17 dans la grille ci-après. En élargissant la grille vers la droite et en appliquant la même régularité, il veut écrire les nombres de 18 à 200.

Quelle sera la position de la case occupée par 200 ?

Récréation 40
Une mouche part du point A. Il y a cinq chemins pour se rendre au point B. De B à C, il y a quatre chemins. De C à D, il y a trois chemins. À partir de A, la mouche se rend à D en passant par B et C.

Combien la mouche pourra-t-elle parcourir de chemins différents pour se rendre de A à D ?

Récréation 41
Dix couples de lapins se rencontrent. Chacun des lapins donne une carotte aux autres lapins, sauf à son partenaire.

Combien de carottes seront données ?

Récréation 42
Samuel trace la grille ci-après et y écrit les nombres 1 et 2. Il veut disposer chacun des nombres de 3 à 16 de telle manière que deux nombres qui se suivent, comme 3 et 4, ne soient jamais voisins horizontalement, verticalement ou en diagonale.

Trouvez une façon de compléter la grille.

Récréation 43
Félix a dessiné un triangle. Il a tracé quatre parallèles à la base, neuf perpendiculaires à cette même base et deux parallèles aux autres côtés.

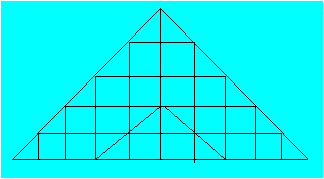
Combien peut-on compter de triangles de toute grandeur dans cette figure ?

Récréation 44
Rose attribue un nombre à chaque lettre selon son rang dans l’alphabet. Elle prend un mot et multiplie les rangs. Cela donne le code du mot. Par exemple le code de ROSE est 18 ´ 15 ´ 19 ´ 5 = 25 650. Voici la correspondance :

Trouvez des mots dont le code est 99 999 ou est le plus près possible de ce nombre.

Récréation 45
Noémie place un cavalier sur chacune des cases marquées C de la grille ci-après. Comme aux échecs, le cavalier se déplace en L.

À partir de leur point de départ, les deux cavaliers pourront-ils visiter toutes les cases non occupées ? Dans le cas où ce ne serait pas possible, combien de cases ne pourront pas être atteintes ?

Récréation 46
Antoine a écrit l'addition ci-après. Il doit remplacer chaque A par un chiffre pair et chaque B par un chiffre impair. Dans cette addition, chacun des chiffres de 0 à 9 doit être pris une seule fois.

AB + AA + BA + BB = ?

Trouvez le plus grand nombre de sommes différentes.

Récréation 47
Zoé trace des croix dans une grille 4 × 4 en suivant les lignes. Les quatre croix montrées ci-dessous occupent des positions différentes et ce sont les quatre seuls cas possibles. Zoé veut tracer des croix de même grandeur dans une grille 12 ´ 12.

Combien peut-on tracer de croix ayant des positions différentes dans une grille 12 ´ 12.

Récréation 48
Une puce part du point à gauche et se dirige vers la droite en suivant le chemin indiqué. Pour elle, un segment parcouru est un puçon. Quand la puce atteint le dernier point montré ci-après, elle continue de se déplacer selon le même modèle.

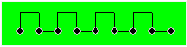
Combien la puce aura-t-elle parcouru de puçons lorsqu’elle s’arrêtera au 99^e point ?

Récréation 49
Jade a formé un carré magique d’ordre 4 avec les nombres de 1 à 16. La somme des nombres horizontalement, verticalement et en diagonale est 34. Voici le carré trouvé par Jade :

Avec les mêmes nombres, complétez le carré suivant pour qu’il soit magique. Le 1 et le 3 sont en bonne position.

Récréation 50
Mia vient de terminer son journal intime. Avant de le mettre sous clef, elle le pagine à partir de 1 jusqu’à la dernière page. Cette tâche étant accomplie, elle compte le nombre de chiffres qu’elle a dû écrire pour la pagination. Ce nombre se termine par 4.

Combien le journal de Mia possède-t-il de pages au minimum ?