|
*********************
Récréations 101 à 150
*********************
Récréation 101
Victor a
placé 24 oranges en un rectangle comme ceci. Il veut compter les carrés
de toute grandeur dont les sommets sont les oranges, y compris ceux qui
peuvent être formés par des traits obliques.

Combien peut-on tracer de carrés
de toute grandeur ?
Récréation 102
Étienne dispose huit pommes comme
ci-après. Sur chaque pomme, il écrit un numéro différent de 1 à 10,
sauf 3 et 4. La somme des numéros de deux ou de trois pommes reliées par
une droite doit être égale à 16.
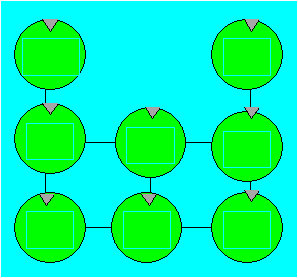
Distribuez les numéros.
Récréation 103
Une tortue part de A. Elle doit passer d’un T à un autre en se déplaçant
horizontalement, verticalement ou obliquement vers le bas sans jamais
revenir vers le haut.
|
T |
T |
A |
T |
T |
|
T |
T |
T |
T |
T |
|
T |
T |
T |
T |
T |
|
T |
T |
T |
T |
T |
|
T |
T |
B |
T |
T |
Combien la tortue peut-elle
emprunter de chemins différents pour se rendre à B ?
Récréation 104
Ambroise a composé un carré
magique le 16 juin 2010. On y trouve d’ailleurs la date.
Complétez le carré pour que la
somme soit la même dans chaque rangée horizontale, verticale et
diagonale.
Récréation 105
Victoria prend 10 timbres et les
numérote comme ceci.
Combien y a-t-il de groupes
différents de trois timbres qui contiennent deux numéros pairs et
un numéro impair ?
Récréation 106
Léo dessine sur du carton deux
rectangles mesurant chacun quatre centimètres de long et trois
centimètres de large. Il trace une diagonale dans chaque rectangle. Par
découpage, il obtient quatre triangles rectangles.
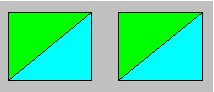
Agencez les quatre pièces de
façon à produire successivement un triangle, un parallélogramme, un
trapèze et un hexagone.
Récréation 107
Léonie prépare six jetons et les
numérote de 1 à 6. Elle dessine la figure ci-après. Elle veut
distribuer les jetons sur les cercles de façon à ce que la somme soit
successivement 9, 10, 11 et 12.
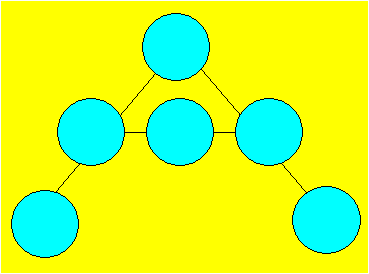
Trouvez au moins une configuration
dans chaque cas.
Récréation 108
Annabelle écrit des nombres de 1
à 4 dans les cases d’une grille 4 ´ 4.
Elle doit compléter la grille avec des nombres de 1 à 4 pour que chaque
nombre apparaisse une seule fois dans chaque ligne et dans chaque colonne.
|
1 |
|
|
2 |
|
2 |
|
|
1 |
|
3 |
|
|
1 |
|
1 |
|
|
2 |
|
|
4 |
1 |
|
|
|
1 |
2 |
|
|
|
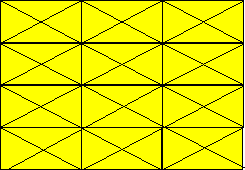
1 |
2 |
|
|
|
2 |
1 |
|
|
|
3 |
2 |
|
|
|
3 |
4 |
|
|
|
3 |
4 |
|
|
|
4 |
3 |
|
|
4 |
|
|
3 |
|
4 |
|
|
3 |
|
4 |
|
|
2 |
|
3 |
|
|
1 |
|
2 |
|
|
3 |
|
3 |
|
|
2 |
|
1 |
|
|
4 |
|
1 |
|
|
4 |
|
|
1 |
2 |
|
|
|
2 |
3 |
|
|
|
2 |
1 |
|
|
|
4 |
1 |
|
|
|
4 |
3 |
|
|
|
4 |
1 |
|
|
|
3 |
4 |
|
|
|
3 |
2 |
|
|
1 |
|
|
4 |
|
1 |
|
|
4 |
|
2 |
|
|
3 |
|
2 |
|
|
3 |
Lequel ou lesquels des huit
carrés peuvent être remplis selon ces règles ?
Récréation 109
Alex a tracé le rectangle
ci-après. Il y a introduit des droites.
Combien peut-on compter de
losanges de toute grandeur dans cette figure ?
Récréation 110
Jérémie prend des quilles et les
numérote : 2, 5, 6, 8, 9, 10, 12, 13 et 16. Il veut placer les
quilles dans une grille 3 ´ 3
pour qu’il y en ait le même nombre dans chaque rangée horizontale,
verticale et diagonale.
Distribuez les neuf quilles.
Récréation 111
Nathan a dessiné le rectangle
ci-après qui est composé de 12 petits carrés.
En suivant les lignes, combien de
rectangles de toute grandeur peut-on compter dans cette figure ?
Récréation 112
Jeanne a représenté les chiffres
de 0 à 9 avec des allumettes.

a) Quel est le plus petit nombre
de trois chiffres qui exige le plus d’allumettes.
b) Quel est le plus grand nombre
de trois chiffres qui exige le moins d’allumettes.
Récréation 113
Rémonde dépose 10 cartes dans le
premier îlot et veut les faire passer au second îlot.
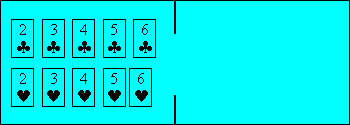
• Quatre cartes doivent passer
ensemble du premier îlot au second. Leur valeur doit être consécutive.
Exemples : 2, 3, 4, 5 ou 3, 4, 5, 6.
• Deux cartes doivent passer
ensemble du second îlot au premier. Elles sont alors toutes deux de
trèfle ou encore toutes deux de cœur.
Trouvez une façon de faire passer
les 10 cartes dans le second îlot.
Récréation 114
Henri a placé des boules noires et
des boules grises comme ci-après. Il décide de tracer des rectangles
dont les quatre sommets sont des boules grises.

Combien Henri peut-il tracer de
rectangles de toute grandeur ?
Récréation 115
En quittant la cour d’école,
Cédric a vu un porc et un veau. Il a alors écrit l’addition suivante
dans laquelle chaque lettre représente un chiffre différent. Lorsque V =
5, il existe 12 valeurs différentes pour COUR.
|
P O R C
+ V E A
U
C O U R |
Trouvez au moins une valeur de
COUR.
Récréation 116
Philippe a découpé huit jetons
numérotés de 1 à 7. Il choisit au hasard quatre jetons et les dépose
sur le tableau qui comprend quatre cases.
Combien le tableau peut-il
contenir de combinaisons différentes ?
Récréation 117
Victoria a tracé cet hexagone.
Elle l’a partagé en petits triangles.
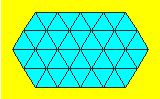
Combien peut-on compter d’hexagones
de toute grandeur dans cette figure ?
Récréation 118
Catherine établit le tableau
suivant qui indique la valeur de chacune des lettres.
|
A
N |
B
O |
C
P |
D
Q |
E
R |
F
S |
G
T |
H
U |
I
V |
J
W |
K
X |
L
Y |
M
Z |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
Le code d’un mot est la somme
des nombres attribués à chaque lettre. Par exemple, le code de BUT est
17.
Trouvez au moins trois mots dont
le code est 29.
Récréation 119
Monsieur W se promène avec madame
X. Ils rencontrent madame Y et monsieur Z. Chacun des quatre personnages a
une tête en forme de quadrilatère.
Monsieur
W déclare : " J'ai deux paires de côtés parallèles et au
moins un angle droit. "
Madame
X déclare : " J'ai quatre côtés de même longueur et aucun
angle droit. "
Madame
Y déclare : " Je n’ai pas d’angle droit. "
Monsieur
Z déclare : " J'ai deux paires différentes de côtés de même
longueur. "
Quelle forme de tête a chaque
personnage parmi le carré, le rectangle, le losange et le
parallélogramme ?
Récréation 120
Marianne écrit les cinq nombres
suivants.
À l’aide d’opérations
simples, combinez les cinq nombres de façon à ce que le résultat soit
256 ou le plus près possible de 256.
Récréation 121
Michelle a compté 13 triangles
dans la première figure : six triangles constitués d'une partie,
quatre de deux parties, deux de trois parties et un de six parties.
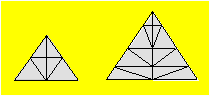
Combien y a-t-il de triangles de
toute grandeur dans la seconde figure ?
Récréation 122
Simon s’amuse avec ses lapins.
Ils sont là : cinq lapins aux yeux gris et cinq autres aux yeux
roux. Il désire disposer cinq lapins en une rangée de telle manière qu’un
lapin aux yeux gris ne soit jamais voisin de deux lapins aux yeux roux.
Combien y a-t-il de façons
différentes de réaliser une telle rangée de cinq lapins ?
Récréation 123
Sara a
écrit l’addition ci-après dans laquelle chaque lettre représente un
chiffre différent. Il y a quatre façons de déchiffrer l’addition
quand I est égal à 2.
|
N E U F
+ O
N Z E
V
I N G T |
Trouvez une de ces égalités.
Récréation 124
Pauline a
écrit les carrés : 1, 4, 9, 16, 25, 36, 49, ... Elle se demande combien
il y a de carrés dans la suite :
3 6 9 12
15 ... 999
Combien y a-t-il de tels
carrés ?
Récréation
125
Prenez huit jetons. Disposez-les
afin d’obtenir
a)
quatre rangées de trois jetons.
b)
cinq rangées de
trois jetons.
c)
six rangées de
trois jetons.
d)
sept rangées de
trois jetons.
Récréation 126
Florence
découpe 15 jetons sur lesquels elle écrit les lettres de la grille
ci-après ; puis elle dépose les jetons sur la lettre correspondante.
|
R |
A |
I |
K |
|
M |
P |
C |
N |
|
L |
U |
O |
D |
|
Z |
R |
T |
|
Elle fait glisser les jetons un par un
sur toute case libre voisine sans les soulever. À la fin, elle doit obtenir les
mots de cette grille.
|
R |
I |
C |
K |
|
P |
L |
A |
N |
|
M |
O |
R |
D |
|
Z |
U |
T |
|
Déplacez les jetons en faisant le moins
de mouvements possible.
Récréation 127
Clara prend les dominos suivants :
(1, 1), (1, 2), (1, 3), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 3), (3, 4),
(3, 5), (4, 4), (4, 5), (5, 5), (5, 6). Elle veut placer les dominos sur le
tableau de façon à ce que chaque chiffre corresponde au nombre de points des
dominos. Les pièces de chaque coin sont en bonne position.
|
1 |
1 |
4 |
2 |
2 |
|
3 |
5 |
3 |
5 |
6 |
|
1 |
5 |
5 |
2 |
1 |
|
2 |
1 |
5 |
5 |
2 |
|
4 |
3 |
5 |
2 |
3 |
|
3 |
3 |
4 |
4 |
4 |
Reconstituez le tableau.
Récréation 128
Mathilde a représenté la figure
ci-après avec des cure-dents. Par la suite, elle a pris son crayon et sa
règle. Pour deux cure-dents ou plus en ligne droite, elle a tracé une droite.
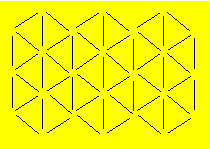
Combien de droites Mathilde a-t-elle
tracé pour construire la figure avec son crayon ?
Récréation 129
Découpez huit jetons. Dessinez un
téléphone sur quatre jetons et un livre sur quatre autres jetons. Placez-les
comme dans ce tableau.
Il s’agit de déplacer deux jetons
voisins sur des cases libres en même temps vers la droite ou vers la gauche. À
la fin, les jetons doivent être regroupés ainsi.
Déplacez les jetons en un minimum de
mouvements.
Récréation 130
Rosalie a
assemblé six triangles équilatéraux comme ci-après. Cette figure a six
côtés. Il existe quatre autres figures formées par six triangles
équilatéraux qui ont six côtés.
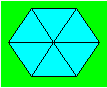
Trouvez au moins deux de ces figures.
Récréation 131
Simon a écrit l’addition ci-après.
Chaque lettre représente un chiffre différent. Dans ce cas, P = 6 et E = 4.
Trouvez la valeur de chaque lettre.
Récréation 132
Clara a dessiné la figure ci-après.
Elle veut y placer chacun des nombres de 1 à 11, sauf 2 et 8. La somme doit
être 16 dans chaque rangée de deux ou trois cellules reliées par une droite.
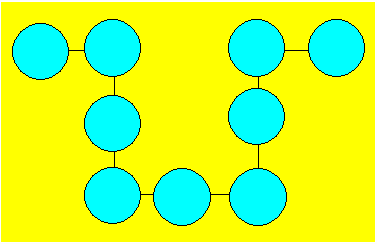
Distribuez les nombres.
Récréation 133
Clara est née le 8 juin 2012. Sa mère
qui adore les carrés magiques veut lui en préparer un. Elle écrit la date de
naissance sur la quatrième ligne : 8 - 6 - 2012. Puis elle remplit la
grille de façon que la somme des nombres de chaque rangée horizontale,
verticale et diagonale soit la même.
Complétez la grille avec des nombres
qui n’arrivent pas nécessairement une seule fois.
Récréation 134
Lydia dispose 20 pièces de monnaie en
quatre rangées de cinq centimes chacune. En partant de n’importe lequel
centime, joignez les pièces sans lever le crayon et sans passer deux fois sur
la même droite. Elle peut ainsi former des rectangles dont les sommets
correspondent à quatre centimes.
¡ ¡
¡ ¡
¡
¡ ¡
¡ ¡
¡
¡ ¡
¡ ¡
¡
¡ ¡
¡ ¡
¡
Combien peut-on construire de rectangles
au maximum ?
Récréation 135
Érika découpe neuf jetons. Sur un
côté, elle écrit chacune des lettres du tableau ci-après. Sur l’autre
côté, elle écrit un nombre choisi parmi les nombres 2, 3, 4, 5, 6 et 7. Ce
faisant, lorsque deux jetons ont la même lettre, il leur attribue le même
nombre.
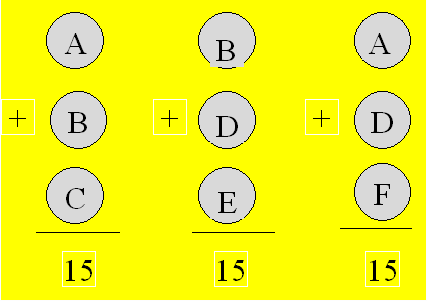
Donnez une valeur numérique à chaque
jeton de façon à ce que la somme soit 15 dans chaque colonne.
Récréation 136
Louis dessine une grille carrée avec des
bâtonnets. Sur le contour, il place des bâtonnets rouges et à l’intérieur
des bleus.
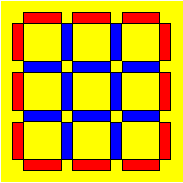
Combien de bâtonnets bleus seront
nécessaires pour former une grille rectangulaire 10 ×
12 ?
Récréation 137
Mathieu a dessiné la figure ci-après.
Il désire y disposer les nombres de 1 à 8 pour que la somme soit 14 dans
chaque rangée de trois cellules reliées par une droite.
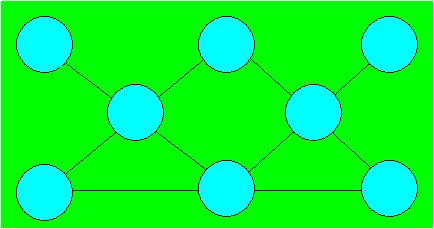
Distribuez les nombres.
Récréation 138
Paulin a dessiné les trois formes
suivantes composées respectivement de 3, 4 et 5 carrés unitaires. Il prend
trois croix et désire construire un rectangle 5 ×
7. Il complète le rectangle avec un certain nombre de pièces des deux autres
formes.

De combien de pièces de chaque autre
forme Paulin a-t-il besoin ?
Récréation 139
Je suis le dernier chiffre de
20132013
Qui suis-je ?
Récréation 140
Maxime a dessiné la figure ci-après. Il
veut disposer chaque nombre de 1 à 8 pour que la somme soit 20 dans chacune des
cinq rangées de trois cellules reliées par une droite. Les nombres 9, 10 et 11
sont en bonne position.
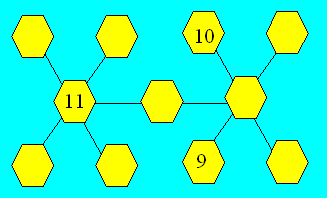
Distribuez les nombres de 1 à 8.
Récréation 141
Clément prend 16 boules de golf et les
numérote de 1 à 16. Dans la grille ci-après, les boules 12, 13, 14, 15 et 16
sont déjà placées. Les cases vertes doivent recevoir des nombres pairs.
Placez les boules pour que la somme des
numéros soit 34 dans chaque rangée horizontale, verticale et diagonale.
Récréation 142
Coccinelle dit à Cafard :
- Retire neuf cartes de ton jeu. Je les ai dessinées pour toi.

- Maintenant, place ces neuf cartes en
un carré. La somme des chiffres doit être 12 dans chaque rangée horizontale,
verticale et diagonale. De plus, il doit y avoir une seule couleur (cœur,
carreau ou trèfle) sur chaque ligne et dans chaque colonne.
Trouvez une disposition des cartes.
Récréation 143
Marius a tracé la figure ci-après d’un
seul trait sans passer plus d’une fois sur une même ligne.
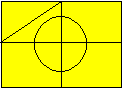
De combien de points le crayon de Marius
peut-il partir ?
Récréation 144
Stanislas a découpé sept triangles
équilatéraux. En les assemblant, il trouve 24 configurations différentes. En
voici quatre :
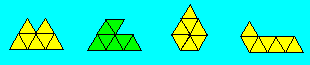
Trouvez au moins quatre autres
configurations.
Récréation 145
Un lièvre part d’une case d’une
grille. Il se déplace horizontalement ou verticalement en deux mouvements. Le
premier mouvement est un pas vers une case voisine. Le second mouvement est un
saut au-dessus d’une case libre ou non. Dans la grille ci-après, huit cases
atteintes sont indiquées.
En partant d’une case de votre choix,
trouvez un chemin qui permet d’atteindre le plus de cases possible.
Récréation 146
Éva a découpé les quatre pièces
ci-après. Celles-ci sont formées respectivement de 3, 5, 4 et 5 petits
carrés.
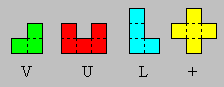
Prenez cinq V, trois U, quatre L et deux
+. Construisez un rectangle 7 × 8.
Récréation 147
Béatrice écrit sur son
bloc-notes :
JEU DE CARTES JEU DE CARTES JEU DE CARTES
JEU DE ...
Elle s'arrête à la lettre de rang
499.
Quelle est cette lettre ?
Récréation 148
Eulalie trace des diagonales dans la
grille ci-après. Elle a ainsi formé des carrés disposés obliquement.

Combien peut-on compter de carrés
obliques de toute grandeur dans cette grille ?
Récréation 149
Jacinthe a préparé quatre
pièces : un carré et trois triangles de même grandeur. Chaque côté du
carré de même que chaque côté de l’angle droit mesurent cinq unités. L’hypoténuse
mesure approximativement sept unités.
Assemblez les quatre pièces pour que le
périmètre mesure 41 unités.
Récréation 150
Philippe choisit six dominos : (1,
3), (1, 4), (2, 3), (3, 4), (2, 5), (3, 5). Il doit placer horizontalement les
dominos sur la grille ci-après. Le total des points doit être 12 dans chaque
rangée horizontale et 6 dans chaque rangée verticale.
Distribuez les neuf dominos.
|
|
![]()
![]()