|
*********************
Récréations 51 à 100
*********************
Récréation 51
Alicia
découpe dans le carton des tuiles de 1 centimètre sur 2 centimètres. Elle
les place de façon à former le contour d’un carré. Par exemple, elle
prend huit tuiles et elle les place comme ci-après. L’aire du carré
intérieur est alors de 9 centimètres carrés.

Une autre fois, Alicia prend 36
tuiles et les place sur le contour de la même façon. Quelle sera alors l’aire
du carré intérieur ?
Récréation 52
Une mouche part de la case 1 sur la
grille ci-après. Elle se déplace en deux mouvements qui se font en
alternance. Le premier mouvement est le saut du cavalier aux échecs, soit
en L. Le suivant est un pas horizontalement ou verticalement. Les cinq
premières cases atteintes sont indiquées.
En partant d’une case de votre
choix, trouvez un chemin qui permet d’atteindre le plus de cases possible.
Récréation 53
Nicolas a acheté 164 blocs-notes
pour le bureau. Ces blocs-notes sont répartis dans trois boîtes. La boîte
A contient deux blocs-notes de plus que la B. Si on enlevait 10 blocs-notes
à la B et si on ajoutait 13 blocs-notes à la C, cette dernière
contiendrait trois fois plus de blocs-notes que la B.
Combien y a-t-il de blocs-notes dans
chacune des boîtes ?
Récréation 54
Maélie veut placer chacun des
nombres de 1 à 8 dans la figure ci-après. La somme des nombres de trois
cercles reliés par une droite doit être la même. Dans cet exemple,
Maélie a obtenu une somme de 12.
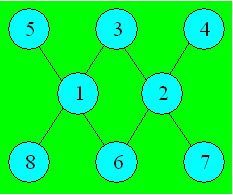
Quelle est la plus grande somme qui
va permettre de distribuer les nombres de 1 à 8 ?
Récréation 55
Justin prend un cavalier et le place
dans la case 1, puis dans la 2, d’une grille rectangulaire comme
ci-après. Comme aux échecs, le cavalier se déplace en L.
Continuez à déplacer le cavalier
pour qu’il visite le plus de cases possible.
Récréation 56
Julie assemble 28 hexagones et
obtient la figure suivante.

Combien d’allumettes seront
nécessaires pour reproduire cette figure ?
Récréation 57
Mathis dessine la figure ci-après
dans laquelle il dispose neuf cases. Il veut y placer chacun des nombres de
1 à 9. La somme doit être 15 dans chaque rangée de trois cases reliées
par une droite.
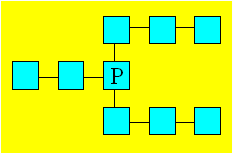
Trouvez une façon de distribuer les
nombres de 1 à 9 pour que la case marquée P contienne un nombre pair.
Récréation
58
Prenez
six jetons. Disposez-les afin d’obtenir
a)
deux rangées de trois jetons chacune.
b)
trois rangées de trois jetons chacune.
c)
quatre rangées de trois jetons chacune.
Récréation 59
Rébecca n’arrive pas à s’endormir.
Il est 1:01, 1:12, 1:21. Le temps passe, mais Rébecca reste éveillée.
Toutefois, elle note que chacune des marques au cadran vues précédemment
est formée de deux chiffres identiques et d’un troisième différent des
deux autres.
De 2 heures à 6 heures
inclusivement, combien de marques d’heures qui se terminent par un chiffre
pair ont ces propriétés ?
Récréation 60
Zildor a découpé les quatre pièces
ci-après. Elles sont formées respectivement de 4, 2, 4 et 4 petits
carrés.
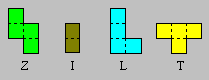
Prenez deux Z, deux I, un L et six
T. Construisez un rectangle 4 ´
10.
Récréation 61
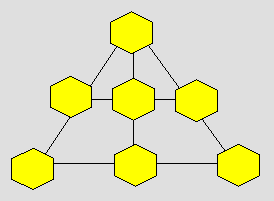
Line prend neuf jetons et les
numérote ainsi : 1, 2, 3, 4, 5, 6, 7, 8, 9. Elle veut placer les jetons sur
les côtés du triangle.
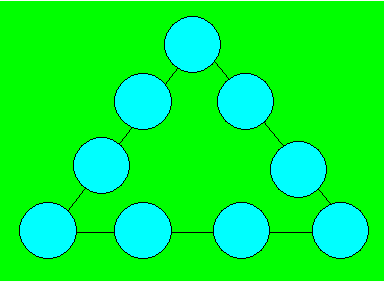
Distribuez les neuf jetons pour que
la somme sur chacun des quatre côtés soit 21.
Récréation 62
Zacharie a tracé la grille
rectangulaire 5 ´ 8
ci-après. Il colorie un T dans le coin supérieur gauche. Il veut remplir
la grille avec d’autres T de même grandeur, mais pouvant être l’objet
de rotation. Aucune partie d’un T ne doit coïncider avec un autre T.
Au maximum, combien peut-on colorier
de T dans cette grille ?
Récréation 63
Bernadette est née le 2 novembre
2010. Sa mère a écrit la date dans la grille carrée suivante.
Complétez la grille pour que la
somme soit la même dans chaque rangée horizontale, verticale et diagonale.
Récréation 64
Dans les cellules, disposez chaque
nombre de 2 à 8 pour que la somme soit 15 dans chacune des cinq rangées de
trois cellules reliées par une droite.
Récréation 65
Alexandra a dessiné un carré 4 ´
4 de points. Elle y a tracé un triangle dont un point
est à l’intérieur.

Combien peut-on tracer d’autres
triangles de même grandeur ayant un point à l’intérieur ?
Récréation 66
Adam découpe six jetons et les
numérote de 1 à 6. Puis il les place sur le tableau suivant.
Il peut déplacer tout jeton en
sautant au-dessus d’une case ou en le glissant sur une case voisine. À la
fin, il doit obtenir ce tableau.
Réalisez ce transfert en ayant soin
de faire le moins de mouvements possible.
Récréation 67
Un calendrier est formé de cinq mois
de 73 jours chacun. Les mois sont : mars, avril, mai, juin et juillet.
Roger se souvient du 1er avril de cette année-là quand on lui
apposa un poisson dans son dos. C’était un mercredi.
Quel jour de la semaine était le 73
juin de cette même année ?
Récréation 68
Une tortue part d’une case d’une
grille 4 ´ 5. Elle
se déplace en deux mouvements qui se font en alternance. Le premier
mouvement est un pas horizontalement ou verticalement. Le suivant est un pas
en diagonale. Dans la grille, huit cases atteintes sont indiquées.
En partant d’une case de votre
choix, trouvez un chemin qui permet d’atteindre le plus de cases possible.
Récréation 69
Quand Madeleine se promène dans les
sentiers pédestres, son pas mesure la demie d’un mètre. En ce jour, elle
s’adonne à un exercice. Elle avance successivement de 30 pas et recule de
10 pas toujours en ligne droite. Elle s’arrête avant le 10e
recul.
Quelle distance Madeleine
aura-t-elle parcourue à ce moment-là ?
Récréation 70
Francis a construit un triangle d’étoiles
comme ci-après. Il le montre à sa jumelle Francine. Celle-ci lui
dit : - Moi, j’ai construit un triangle d’étoiles sur le même
modèle. Après cela, j’ai disposé toutes mes étoiles en rangées de
huit. Une seule étoile n’a pas pu être placée.
L
L
L
L
L L
L
L L L
L
L L L
L
L
L L L
L L
Au minimum, combien d’étoiles
contenait le triangle de Francine ?
Récréation 71
Marcellus a placé dans un bocal un
certain nombre de boules qui valent 5, 10 et 25 points. Il dit à sa sœur Régina
: - Tu dois prendre 20 boules qui totalisent 200 points.
Combien de boules de chaque valeur
la sœur de Marcellus devra-t-elle prendre ?
Récréation 72
Laval a un prénom palindrome puisqu’il
peut être lu dans les deux sens. Il existe aussi des nombres palindromes
comme 85 658. De 100 à 999, on compte 90 nombres palindromes.
Combien existent-ils de nombres
palindromes de 1000 à 9999 ?
Récréation 73
Un fou avance d’une seule case à
la fois en diagonale. Lorsqu’il atteint une case d’un coin, il se
déplace vers une case voisine horizontalement ou verticalement. Le fou part
de la case 1 et peut toucher une seule fois à une case.
Trouvez un chemin qui permet au fou
de parcourir le plus de cases possible.
Récréation 74
Dans un coin du marché d’alimentation,
il y a trois boîtes de radis.
• Si on mettait ensemble deux fois
les radis de la boîte R et ceux de la boîte D, on aurait 84 radis.
• Si on mettait ensemble trois
fois les radis de la boîte D et ceux de la boîte S, on aurait 84 radis.
• Si on mettait ensemble deux fois
les radis de la boîte D et trois fois ceux de la boîte S, on aurait 84
radis.
Combien y a-t-il de radis en tout
dans les trois boîtes ?
Récréation 75
Sophia place au mur la feuille de
calendrier d’un mois de février. Elle doit lancer trois dards sur le
tableau de telle manière que la somme des numéros atteints est 31.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
29 |
|
|
|
|
|
|
Combien y a-t-il de groupes de trois cases qui
permettent une somme de 31 ?
Récréation 76
Laurie dispose 12 citrouilles comme
ci-après. Il les joint par des traits.
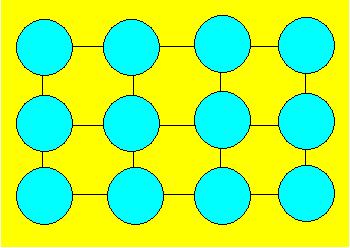
Combien peut-on compter de groupes
différents de trois citrouilles voisines ?
Récréation 77
Dans le tableau ci-après, Arthur a
écrit les nombres de 1 à 27 en serpentant. Selon la même régularité, il
désire écrire la suite des nombres en ajoutant au besoin des lignes et des
colonnes.
|
1 |
4 |
5 |
16 |
17 |
|
2 |
3 |
6 |
15 |
18 |
|
9 |
8 |
7 |
14 |
19 |
|
10 |
11 |
12 |
13 |
20 |
|
25 |
24 |
23 |
22 |
21 |
|
26 |
27 |
|
|
|
Dans quelle position apparaîtra
199 ?
Récréation 78
Julie sort son jeu d’échecs. Elle
prend un cavalier et délimite un carré 5 ´
5 sur l’échiquier. Elle déplace le cavalier de la
case 1 à 4 comme ci-dessous.
Le cavalier de Julie pourra-t-il
atteindre la case grise au 13e saut ?
Récréation 79
Annie a écrit : SEPT, HUIT, DIX
et CENT. Elle combine deux ou trois de ces mots pour former des nombres.
Combien Annie peut-elle former de
nombres ?
Récréation 80
Charlotte découpe cinq jetons. Elle
écrit un nombre sur un côté de chaque jeton et un deuxième sur l’autre
côté.
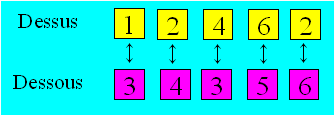
Au minimum, combien faut-il
retourner de jetons pour que la somme des numéros soit la même autant en
dessus qu’en dessous.
Récréation 81
Constantin écrit les cinq nombres
suivants.
5 6 7 9
13
À l’aide d’opérations simples,
représentez 20 ou le plus près de 20 en utilisant ces cinq nombres.
Récréation
82
Prenez sept jetons.
Disposez-les afin d’obtenir
a)
quatre rangées de trois jetons.
b)
cinq rangées de trois jetons.
c)
six rangées de trois jetons.
Récréation 83
Clément rêve d’un ciel beau et
vrai. Il a écrit l’addition ci-après dans laquelle chaque lettre
représente un chiffre différent. Le ciel lui a suggéré d’indiquer que
E = 0 et B = 3.
|
B E A U
+ V R A I
C I E L |
Trouvez une valeur de CIEL.
Récréation 84
Lucas a écrit les lettres de son
prénom dans la grille ci-après. On peut lire ce mot en suivant les lettres
qui se touchent horizontalement et verticalement en tout sens.
|
C |
U |
L |
U |
C |
|
A |
L |
U |
C |
A |
|
S |
U |
C |
A |
S |
|
A |
C |
A |
S |
|
|
|
A |
S |
|
|
Combien de fois peut-on lire LUCAS
dans cette grille ?
Récréation 85
Nicolas a préparé une grille 6 ´
6 comme ci-après. Il a tracé neuf carrés composés
de quatre triangles à l’aide de droites obliques.
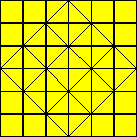
Combien peut-on former de carrés
obliques de cette même grandeur dans une grille 12 ´
12 ?
Récréation 86
Gabrielle dessine la figure suivante.
Elle veut y placer chacun des nombres de 1 à 11, sauf 3 et 5. La somme des
nombres de deux ou de trois cases reliées par une droite doit être égale
à 16.
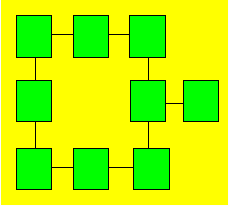
Trouvez une façon de distribuer les
nombres.
Récréation 87
Marguerite s’adresse à sa
nièce :
- Nous sommes en 2013. Je me souviens de la dernière année où le 1er
janvier et le 1er avril étaient un mardi. D’ailleurs, dans ma
vie, c’est arrivé un an avant ma naissance et par après deux fois.
Quel est l’âge de
Marguerite ?
Récréation 88
Adam dessine 31 rangées de fourmis
en augmentant d’une fourmi d’une rangée à l’autre. Voici les cinq
premières rangées :
|
g
g
g
g
g g
g
g g
g
g
g g
g g |
Dans chaque rangée ayant un nombre
pair de fourmis, Adam dessine un A sur le dos de la fourmi qui y occupe un
rang impair. Dans chaque rangée impaire, Adam dessine un A sur le dos de la
fourmi qui y occupe un rang pair.
Combien Adam dessinera-t-il de
A ?
Récréation 89
Théo veut placer chacun des chiffres
de 1 à 8 dans les cases vides du tableau.
Combien y a-t-il des groupes de
quatre nombres dont la somme est 180 ?
Récréation 90
Jérémie dessine quatre triangles
tronqués de boules comme ci-dessous.
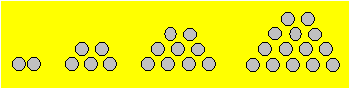
Il continue à dessiner d’autres
triangles tronqués selon le même modèle.
Combien de boules seront
nécessaires pour dessiner le 49e triangle ?
Récréation 91
Émile écrit les chiffres de 0 à 9
avec des cure-dents comme ci-après.
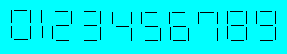
Trouvez cinq nombres d’au plus
cinq chiffres qu’il est possible d’écrire en utilisant 24 cure-dents.
Récréation 92
Alexia numérote neuf balles de 1 à
9. Elle veut placer les balles de façon à ce que la somme des numéros
soit 15 dans chaque rangée de deux ou de trois balles.
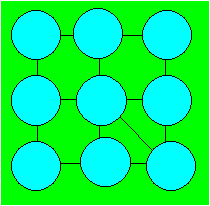
Distribuez les balles.
Récréation 93
Vincent fait la somme des nombres
pairs consécutifs. Il écrit :
|
2
2
+ 4 = 6
2
+ 4 + 6 = 12
2
+ 4 + 6 + 8 = 20
2
+ 4 + 6 + 8 + 10 = 30 |
Quelle est la somme des nombres
pairs consécutifs de 12 à 200 inclusivement ?
Récréation 94
Dans une cour d’école, Coralie
trace un carré dans le sable. Elle place respectivement 4, 5, 6 et 7
élèves sur chaque côté. Chaque élève lance un ballon rouge aux
élèves des trois autres côtés et reçoit d’eux deux ballons bleus.
Ceux d’un même côté ne se lancent pas de ballons.
En tout, combien de ballons seront
lancés ?
Récréation 95
Tristan utilise chacun des chiffres
de 1 à 6 pour réaliser une addition de trois nombres de deux chiffres. La
somme est un nombre de trois chiffres.

Combien y a-t-il de sommes possibles
?
Récréation 96
Vous voulez fabriquer des
casse-têtes géométriques. Vous pouvez procéder ainsi :
De leur côté, chaque élève dessine un carré. Il trace des droites dans
le carré de façon à obtenir six ou sept pièces. Il découpe les pièces.
Puis, il les donne à un autre élève en lui demandant de former un carré.
Récréation 97
Maxime découpe six jetons et les
numérote comme ci-après. Il prend deux jetons à la fois et multiplie
les nombres qui y apparaissent.
Combien peut-on compter de
produits différents ?
Récréation 98
Rosalie écrit quatre nombres : 40,
60, 80, 100. Elle calcule 20 % d’un de ces nombres, 25 % d’un autre, 30
% d’un troisième et 40 % d’un quatrième. Ces quatre résultats forment
un quadruplet. Rosalie additionne les nombres du quadruplet.
Combien y a-t-il de quadruplets dont
la somme est impaire ?
Récréation 99
Zack forme une grille carrée 3 ´
3 avec des cure-dents. Il a besoin de 24 cure-dents.

Combien de grilles carrées Zack
pourra-t-il former s’il utilise pour chaque grille entre 200 et 300
cure-dents ?
Récréation 100
Éve écrit les lettres ci-après
avec des bâtonnets.
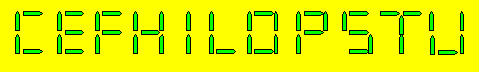
Trouvez, si possible, des mots qui utilisent
successivement 15, 16, 17, 18, 19 ou 20 bâtonnets.
|
![]()
![]()