|
| |
|

|
Récréations
géométriques |
|
Série A
68. À vos cubes
Cubomane prend une boîte remplie de 1000 cubes. Il commence
par disposer ses cubes comme ci-dessous : un premier étage de deux cubes,
deux étages de trois cubes, trois étages de quatre cubes et quatre étages de
cinq cubes.
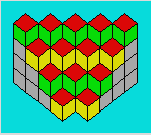
Cubomane continue à disposer ses cubes selon la même
régularité. Combien d’étages entiers Cubomane pourra-t-il construire sur la
dernière rangée en utilisant ses 1000 cubes ?
Solution
|
La
théorie des permutations figurées
s'applique notamment au problème des huit tours aux échecs.
|
|
Série B
68. Sommets de
Léonie
Léonie attribue une valeur
à chacun des sommets d’un rectangle. Par exemple, dans le rectangle suivant,
les valeurs sont 2, 4, 9, 6 et leur somme est 21. Les différences successives
sont 2, 5, 3 et 4.
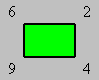
En adoptant les mêmes différences successives, trouvez les
valeurs d’un rectangle dont la somme des sommets est 45.
Solution
|
Si
une énigme est trop tordue, l’intérêt diminue, car le champ de
recherche de solutions est trop vaste ou est difficile à définir.
|
|
Série C
68.
Un rectangle
Prenez
deux A, deux B, trois C, trois E et un F.
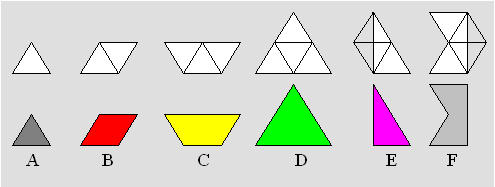
Construisez un rectangle presque carré.
Solution
© Charles-É. Jean
|
De
R à Z, combien de lettres majuscules peuvent être formées au moyen de
cinq traits droits ?
Solution
|
| |
|
|
![]()
![]()