Série A

Solution 59

Les combinaisons de trois nombres dont la somme est 13 sont : (1, 5, 7), (2, 4, 7), (2, 5, 6) et  (3, 4, 6). Dans la figure donnée, il doit y avoir cinq rangées dont la somme est 13. Il manque une combinaison. C’est donc impossible. 

C’est le cousin qui a raison.

Retour au problème

Série B

Solution 59

Dans les cases A2 et E4 doit apparaître un 3. Comme la somme des deux nombres devant être placés dans les deux cases marquées d’une cloche est 8, on place 5 en A3. Puis successivement 4 en A4, 5 en C4, 2 en C5, 1 en C2, 2 en E2, 4 en C1, 2 en D3, 3 en D1, 2 en D3, etc. Voici cette grille complétée :

Retour au problème

Série C

Solution 59

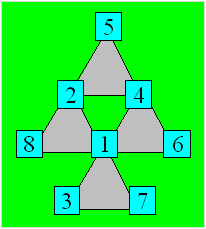
Les combinaisons de trois nombres dont la somme est 11 sont : (1, 2, 8), (1, 3, 7), (1, 4, 6), (2, 3, 6), (2, 4, 5). Une configuration est :

Retour au problème