On pense que les multiparfaits du triparfait à
l'heptaparfait ont tous été trouvés. Tous les nombres multiparfaits connus sont
pairs. On se demande s'il existe des nombres multiparfaits impairs. Voici
une façon de trouver des nombres multiparfaits :
1. On écrit un
nombre premier élevé à une puissance.
2. On trouve la somme
des diviseurs de cette expression.
3. On décompose
cette somme en nombres premiers, s’il y a lieu, et on écrit le résultat au
dénominateur de cette fraction.
4a. Lorsque le
dénominateur est un nombre premier, on écrit ce nombre comme numérateur d’une
autre fraction.
4b. Lorsque le
dénominateur n’est pas un nombre premier, on choisit un ou des facteurs qu’on
écrit comme numérateur de toute autre fraction.
5. On continue ainsi
jusqu’à ce que le produit des fractions soit égal à 1/n. Si n
= 2, le nombre est biparfait ; si n = 3, le nombre est triparfait,
etc.
6. On multiplie les numérateurs
pour obtenir un nombre multiparfait.
Dans le premier
exemple, le produit des numérateurs est 672. Ce nombre est triparfait car l’expression
est égale à 1/3. Dans le deuxième exemple, le produit des numérateurs est 32
760. Ce nombre est tétraparfait car l’expression est égale à 1/4.
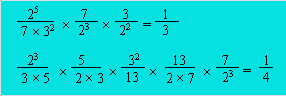
© Charles-É. Jean
![]()
![]()