|
Série A
53. Quilles qui divisent
Quatre quilleuses font le bilan de leur année à ce sport.
Chacune a joué un nombre de parties qui est en relation avec les diviseurs du
nombre correspondant. Le nombre de parties de Colette a trois diviseurs ;
celui de Diane quatre diviseurs ; celui d’Éveline cinq diviseurs ;
celui de Florida six diviseurs. Par exemple, 55 a quatre diviseurs : 1, 5,
11 et 55.
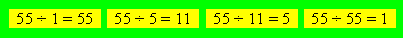
Ainsi, 55 pourrait être le nombre de parties jouées par
Diane, mais ce n’est pas le cas. En effet, chacun des nombres de parties peut
être divisé par 3 sans reste. On sait que Diane et Florida ont joué entre 40
et 60 parties et que les quatre femmes ont joué en tout 186 parties.
Combien
chaque femme a-t-elle joué de parties de quilles ?
Solution
|
Un
solide
enchanté est un arrangement de nombres
disposés sur les sommets d'un solide de telle manière que la somme des
nombres est la même sur chaque face.
|
|
Série B
53.
Adam et Ève
 Adam
et Ève sont frère et sœur. Quand Adam est né, Ève avait 14 ans. Ce matin, Adam écrit son âge sur une ardoise. Ève prend la craie et fait de même.
Adam additionne les âges et dit :
- À nous deux, nous avons 100 ans.
Quel est l’âge d’Ève ?
Solution
|
À
l’aide d’opérations simples, représentez 24 avec trois 3.
Solution
|
|
Série
C
53.
Défi de Jacob
On
a demandé à Jacob de trouver la somme des chiffres des nombres de 1 à 29.
Voici ce qu’il a écrit : "De 1 à 9, la somme des chiffres est 45.
De 10 à 19, la somme des dizaines est 10, celle des unités est 45. De 20 à
29, la somme des dizaines est 20, celle des unités est 45. On fait : 45 ´
3 = 135 ; 10 + 20 = 30 ; 135 + 30 = 165. La somme des chiffres est
165."
Créez un algorithme qui permet de trouver la somme des
chiffres de 0 à N où N est un nombre inférieur à 100. Il s’agit de trouver
une démarche qui est la même pour tout N.
Solution
© Charles-É. Jean
|
Il
existe une stratégie de résolution de problèmes qui consiste à
construire un diagramme.
|
