|
Diagramme
u
Construire un diagramme.
– Stratégie
de résolution de problèmes qui consiste à représenter
graphiquement une situation ou des ensembles d’objets. Le diagramme permet d’illustrer
les données du problème et de les placer en interrelation.
Parmi les
diagrammes, mentionnons celui de Carroll, celui de Venn, le diagramme
cartésien, le diagramme sagittal, le diagramme à branches ou arbre et les
diagrammes utilisés en statistiques comme celui à bandes et le circulaire.
Cette stratégie en est une de représentation.
Problème 1. Dans une école, 101 élèves étudient la musique, 94 l’art
dramatique et 85 le cinéma. Parmi eux, 35 de ces élèves étudient la musique
et le cinéma, 33 la musique et l’art dramatique, 32 l’art dramatique et le
cinéma. Aussi, 12 élèves sont inscrits aux trois matières. Quel est le
nombre d'élèves de cette école ?
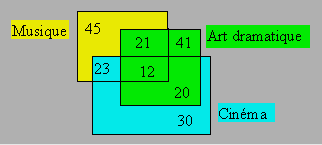
Démarche. On construit un diagramme de Venn. On place 12 à l’intersection
des trois rectangles. Puisque 35 élèves étudient la musique et le cinéma, il y
en a 23 en plus des 12. Puisque 33 élèves étudient la musique et l’art
dramatique, il y en a 21 en plus des 12. On continue ainsi, en soustrayant le
nombre d’élèves déjà compté. Il y a 192 élèves dans cette école.
Le problème aurait pu être résolu en appliquant la formule
suivante : Soit x le nombre d’élèves ayant une seule matière, y
le nombre d’élèves ayant deux matières, z le nombre d’élèves
ayant trois matières et n le nombre d’élèves de l’école,
alors : n = x - y + z.
Cette équation peut
être traduite par la proposition suivante : Le nombre d’élèves de l’école
est égal à la différence du nombre d’élèves ayant une seule matière et
du nombre d’élèves ayant deux matières, à laquelle différence on
additionne le nombre d’élèves ayant trois matières.
Problème 2. À l’occasion d’une fête, cinq amis se donnent
mutuellement un cadeau. Combien de cadeaux seront échangés ?
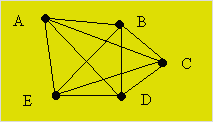
Démarche. Dans le diagramme ci-dessous, chaque ligne représente deux
cadeaux : un donné et un autre reçu. Il y a 10 lignes. D’où, 20
cadeaux furent échangés.
© Charles-É. Jean
Index
: D
|
![]()
![]()