Série A

84. Moutons de Collin

Collin a reçu en héritage la ferme familiale qui, de bovine, est devenue ovine. La terre de Collin est partagée en quatre parties : deux parties au nord marquées NO et NE, deux parties au sud marquées SO et SE.

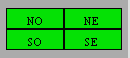
1. Il y a 625 moutons dans les parties du nord : NO et NE.

2. Il y a 958 moutons dans les parties du sud : SO et SE.

3. Il y a 994 moutons dans les parties de l’est : NE et SE.

4. L'unité du nombre de moutons du NO est 3.

5. Le nombre de moutons dans chacune des quatre parties est formé des mêmes trois chiffres différents répartis autrement.

Trouvez le nombre de moutons dans chacune des quatre parties.

Solution

Série B

84. Fleurs de Flore

Flore prépare des rangées de fleurs.

1. Elle met deux fleurs de plus dans la deuxième rangée que dans la première.

2. Elle met trois fleurs de plus dans la troisième rangée que dans la deuxième.

3. Elle met quatre fleurs de plus dans la quatrième rangée que dans la troisième.

Elle a jusqu’à maintenant placé 64 fleurs. 

Combien y aura-t-il de fleurs dans la quatrième rangée ?

Solution

Série C

84. Parité d’Ignace

On partage généralement les nombres en deux classes : les impairs et les pairs. Ignace a décidé de donner aux nombres une parité détaillée. Voici comment il a traduit les nombres de 2 à 12 :