1^e En arithmétique, le carré d’un nombre s’obtient en multipliant un nombre par lui-même. Exemple : 1/4 × 1/4 = 1/16. D’où, 1/16 est le carré de 1/4. Quand on multiplie des entiers, le carré est dit parfait. Par exemple, 7 × 7 = 49. D’où, 49 est un carré parfait. 

Soit une grille carrée 3 × 3 dans laquelle les éléments de chacune des huit rangées ont le même produit, si on divise par un même nombre, on obtient une seconde grille carrée ayant la même propriété. Voici un exemple :

Dans la première grille carrée, le produit est 512 ; dans la seconde, le produit est 8.

Pour élever mentalement au carré les nombres de 6 à 9, on procède ainsi :
6² = (6 + 4)(6 - 4) + 4² = 36                                     7² = (7 + 3)(7 - 3) + 3² = 49
8² = (8 + 2)(8 - 2) + 2² = 64                                     9² = (9 + 1)(9 - 1) + 1² = 81

2^e En géométrie, quadrilatère régulier possédant les propriétés suivantes :

1. Les quatre côtés sont congrus.

2. Les côtés opposés sont parallèles.

3. Les quatre angles sont droits.

4. Les deux diagonales sont congrues. Elles se coupent en leur milieu et à angles droits.

5. Le carré possède quatre axes de symétrie.

Périmètre du carré
Le périmètre d’un carré s’obtient en multipliant par 4 la mesure d’un côté. Si le côté mesure six centimètres, le périmètre est de 4 × 6 = 24 centimètres. Le rapport du périmètre du carré et de la mesure d’une diagonale est égal à une constante qui est approximativement 2,83.

Aire du carré
L’aire d’un carré est le carré de la mesure d’un côté. Si le côté mesure six centimètres, l’aire est de 6 × 6 = 36 centimètres carrés.

Tracé d’un carré
Pour construire un carré dont un côté n’est pas parallèle au plan, on peut procéder des trois façons suivantes :

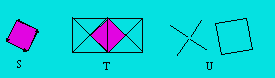
1. On trace un premier segment obliquement. On trace un deuxième segment adjacent et à angle droit de même longueur que le premier ; un troisième et un quatrième toujours à angle droit et de même longueur que les premiers (figure S ci-après).

2. On accole deux carrés de même grandeur par un côté. On trace les deux diagonales de chaque carré. On efface le côté commun. Le petit carré apparaît au centre de la figure T.

3. On dessine deux perpendiculaires de même longueur qui se coupent en leur milieu. On joint les points extrêmes des deux perpendiculaires (figure U).

Moitié d’aire
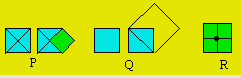
Pour construire un carré dont l’aire est la moitié d’un carré donné, on trace les diagonales. Le côté du carré est la moitié de la diagonale. On complète le carré (figure P ci-après).

Double d’aire
Pour construire un carré dont l’aire est le double d’un carré donné, on trace une diagonale. On prend cette diagonale comme côté du nouveau carré. On complète le carré (figure Q). Dans la construction, une illusion d’optique fait croire que la diagonale est plus courte que tout autre côté du grand carré.

Pavage de carrés
Un des trois pavages de polygones réguliers identiques prend forme avec quatre carrés. En effet, dans la figure R, on peut compter 360 degrés autour de leur point commun.

© Charles-É. Jean