Carré

1^e Produit de deux facteurs égaux. Lorsque les deux facteurs sont des entiers naturels, le carré est dit parfait ou encore est appelé nombre carré. Après avoir énoncé que la somme des deux carrés 4 et 9 était 13, Diophante (v. 325 - v. 410) demanda de trouver deux autres carrés dont la somme est également 13. Les nombres cherchés sont 1/25 et 324/25. 

n Le carré de la somme de deux nombres est égal au carré du premier, plus deux fois le produit du premier par le second, plus le carré du second nombre. Par exemple, le carré de (8 + 5) est égal à : 64 + 80 + 25 = 169.    

n Si un nombre a deux chiffres, son carré est égal au carré des dizaines, plus deux fois le produit des dizaines par les unités, plus le carré des unités. Par exemple, le carré de 85 est égal à : 80² + 2 × 80 × 5 + 5² = 7225. Si un nombre a plus de deux chiffres, on peut le décomposer en deux parties, l’une étant assimilée aux dizaines et l’autre aux unités. On applique alors l’algorithme donné. Par exemple, le carré de 726 (700 + 26) est égal à : 490 000 + 36 400 + 676 = 527 076.

n La différence des carrés de deux entiers consécutifs est égale
1^er à la somme des deux bases. Par exemple, la différence du carré de 24 et du carré de 23 est égale à : 24 + 23 = 47.

2^e au double du petit nombre auquel on additionne 1. Par exemple, la différence du carré de 24 et du carré de 23 est égale à : 23 × 2 + 1 = 47.

3^e au double du grand nombre auquel on soustrait 1. Par exemple, la différence du carré de 24 et du carré de 23 est égale à : 24 × 2 - 1 = 47.

n Quand on connaît le carré d’un entier n, on peut obtenir le carré de (n - 1) en soustrayant (2n - 1) de n². Par exemple, on sait que 24² = 576, le carré de 23 est égal à : 576 - 47 = 529.

n Quand on connaît le carré d’un entier n, on peut obtenir le carré de (n + 1) en additionnant n² et (2n + 1)^. Par exemple, on sait que 24² = 576, le carré de 25 est égal à : 576 + 49 = 625.

n Quand on connaît le carré d’un entier n, on peut obtenir le carré de (n - 2) en soustrayant (4n - 4) de n². Par exemple, on sait que 24² = 576, le carré de 22 est égal à : 576 - 92 = 484.

n Quand on connaît le carré d’un entier n, on peut obtenir le carré de (n + 2) en additionnant n² et (4n + 4). Par exemple, on sait que 24² = 576, le carré de 26 est égal à : 576 +100 = 676.

n À partir de la première identité ci-dessous, on peut établir d’autres identités en combinant les bases des carrés.

n La différence de deux carrés de rangs (n + 2) et n est égale à 4(n + 1). Par exemple, si n = 4, on a : 6² - 4² = 20 = 4 × 5.

n La différence de deux carrés de rangs (2n + 5) et (2n + 1) est égale à 8(2n + 3). Par exemple, si n = 4, on a : 13² - 9² = 88 = 8 × 11.

n Soit A la somme de deux carrés de rangs (2n + 3) et (2n + 7), soit B la somme de deux carrés de rangs (2n + 1) et (2n + 5), alors A - B = 16(n + 2). Par exemple, si n = 4, on a : A = 11² + 15² = 346, B = 9² + 13² = 250, alors A - B = 96 = 16 × 6.

n Soit A la somme de deux carrés de rangs (2n + 2) et (2n + 6), soit B la somme de deux carrés de rangs 2n et (2n + 4), alors A - B = 8(2n + 3). Par exemple, si n = 4, on a : A = 10² + 14² = 296, B = 8² + 12² = 208, alors A - B = 88 = 8 × 11.

n Dans Amusements mathématiques, en 1749, André-Joseph Penckoucke a présenté un procédé pour trouver trois carrés dont la somme est aussi un carré. Voici la façon de procéder :

n Un nombre étant donné, on peut faire la somme des carrés de ses chiffres et répéter la même opération sur le résultat obtenu. Par exemple, si le premier terme est 45, le deuxième sera 4² + 5² = 41, le troisième 4² + 1² = 17 et ainsi de suite. Le tableau suivant donne la séquence de nombres lorsque le nombre initial varie de 1 à 24.

Tous les nombres de ce tableau appartiennent à deux cycles différents : (1, 1) et le cycle C qui est illustré ci-dessous.

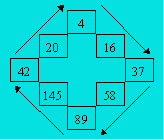
Les nombres inférieurs à 100 qui conduisent directement à ce cycle sont : 2, 24, 40, 61, 73, 85, 98. 

* * * * * * *

2^e Comme figure géométrique, le carré est un polygone qui prend une large place dans la littérature récréative. On le considère comme la figure la plus parfaite, à cause de sa forme simple et de la propriété qu’il possède de se reproduire indéfiniment dans le plan. Il est la base de la configuration du tablier de nombreux jeux comme l'échiquier et le damier. La composition d'un carré au moyen de carrés congruents ou non relève du domaine récréatif. On peut construire notamment un carré avec respectivement deux, trois ou quatre carrés congruents, comme indiqué ci-dessous.

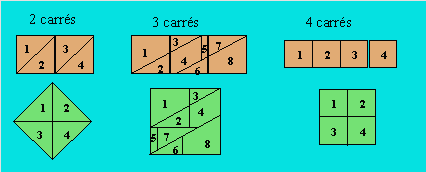
Voici deux autres façons d’obtenir un carré à partir de trois carrés :
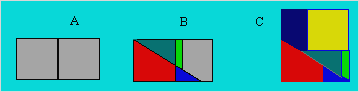
1^er On accole deux carrés (figure A). On les partage comme il est illustré en B. On assemble les six pièces obtenues autour du carré qui reste. On obtient le carré C qui est composé de six pièces.

2^e On prend deux carrés. On trace une diagonale dans chaque carré et on découpe chaque carré en deux pièces en suivant la diagonale. On dispose les pièces obtenues le long du troisième carré de telle sorte que la diagonale touche au carré et qu’aucun triangle n’empiète l’un sur l’autre.

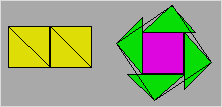
On trace une droite qui relie deux sommets consécutifs des angles droits des triangles. On découpe la partie excédentaire ; celle-ci comble l’espace vide entre la droite et l’autre triangle. On obtient ainsi un carré composé de neuf pièces.

Le carré est l'objet de dissection. Il peut être découpé en un nombre minimum n de pièces qui sont alors assemblées pour former chacune des figures indiquées. Sauf les croix, les polygones sont réguliers.

Le tableau suivant contient les 10 plus petits nombres pour chacune des classes de nombres figurés reliés au carré. La dimension D est donnée pour chaque classe.

Deux carrés ayant chacun n unités de côté assemblés avec deux carrés ayant chacun (n + 1) unités de côté forment un carré ayant (2n + 1) unités de côté à la condition que deux carrés unitaires coïncident au centre du grand carré. Voici un carré dans lequel on a deux carrés 4 × 4 et deux carrés 5 × 5 :

Toute figure carrée pavée de petits carrés congruents et juxtaposés côté à côté est appelée, par extension, carré. L'arithmétique et la géométrie s'unissent quand on place des nombres, des lettres ou des symboles dans les petits carrés, selon des règles variées. 

Les carrés magiques à eux seuls ont fait l'objet de nombreux travaux. Les carrés formés de nombres reçoivent une appellation en fonction des règles d'arrangement des éléments.

Les classes de carrés mentionnées dans ce dictionnaire sont :

3^e Au poker, combinaison des quatre cartes de la même couleur : quatre rois, par exemple.

© Charles-É. Jean

Index : C