Cercle

Ensemble de tous les points du plan qui sont également distants d’un point donné appelé centre. Le cercle peut être considéré comme la limite d’un polygone régulier ayant un nombre infini de côtés. Trois points non alignés déterminent un et un seul cercle. Les principaux termes reliés au cercle sont définis ainsi :

Rayon
Segment de droite qui relie le centre du cercle à un de ses points, comme OA dans l’exemple ci- après.

Diamètre
Segment qui passe par le centre du cercle et dont les deux extrémités sont sur le cercle, comme BC ci-après. Le diamètre partage le cercle en deux parties de même aire. La longueur du diamètre est le double de celle du rayon. Tous les diamètres d'un cercle sont congrus.

Arc
Portion de cercle limitée par deux points du cercle, comme AH, BD et EC. Dans un cercle, l'angle au centre a pour mesure la mesure de l'arc compris entre ses côtés.

Corde
Segment de droite qui relie deux points du cercle, comme DE. Toutes les médiatrices des cordes d'un cercle se rencontrent au centre du cercle.

Sécante
Droite qui coupe le cercle en deux points comme DE. La sécante est une droite prolongée.

Tangente
Droite qui touche le cercle en un seul point comme FG qui passe par H.

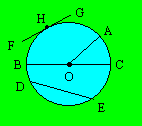
Disque
Région du plan limitée par un cercle. La partie bleue est le disque.

Circonférence
Longueur du cercle. C’est son périmètre. Le rapport de la circonférence au diamètre est constant ; il est égal à p ou approximativement à 3,1416. En d’autres mots, la circonférence mesure un peu plus de trois fois le diamètre. 

Si le diamètre est de 12 centimètres, la circonférence est légèrement supérieure à 36 centimètres, soit 12p = 37,7 centimètres. D’où, la circonférence est égale au produit du diamètre et de p ou encore au produit du double du rayon et de p. Soit C la circonférence et R le rayon, C = 2pR.

Aire du cercle
L’aire du cercle est égale au produit de p et du carré du rayon. Soit A l’aire du cercle et R le rayon, A = pR².

Secteur circulaire
Surface comprise entre un arc et les rayons qui joignent ses extrémités. AOB est un secteur circulaire (figure P ci-après). Soit d la mesure de l’angle au centre et A l’aire du cercle, l’aire du secteur circulaire est égale à A × d/360. 

Par exemple, si l’angle au centre mesure 40 degrés et que l’aire du cercle est 36 cm², l’aire du secteur est 36 × 40/360 = 4 cm². En d’autres mots, l’aire d’un secteur est à l’aire du disque comme la mesure de l’angle au centre l’est à la circonférence qui est établie à 360 degrés par convention. 

On peut aussi obtenir l’aire d’un secteur circulaire en multipliant la longueur de l’arc par la moitié du rayon.

Segment circulaire
Surface comprise entre un arc et la corde qui joint ses extrémités. Dans la figure Q, CDE est un segment circulaire. L’aire d’un segment circulaire est égale à différence de l’aire du secteur circulaire correspondant et l’aire du triangle dont le sommet est au centre du cercle et dont la base est la corde du segment. L’aire de CDE = aire de COED - aire de COE (figure R).

Couronne circulaire
Surface comprise entre deux cercles concentriques. La largeur de la couronne est la différence de la mesure des rayons des deux cercles. L’aire de la couronne est la différence de l’aire du grand cercle et du petit (figure S).

On peut partager un cercle en un nombre minimal de parties. Voici ce qui se passe quand on trace les quatre premières droites :

On remarque qu’il y a une augmentation de deux parties pour le deuxième cercle par rapport au premier, une augmentation de trois parties pour le troisième cercle par rapport au deuxième et une augmentation de quatre parties pour le quatrième cercle par rapport au troisième. On peut exprimer cela ainsi : 1^er cercle : 2 parties ; 2^e cercle : 2 + 2 = 4 parties ; 3^e cercle : 2 + 2 + 3 = 7 parties ; 4^e cercle : 2 + 2 + 3 + 4 = 11 parties, etc.

* * * * * * * * *

Vous trouverez ci-dessous huit problèmes. Les solutions sont données à la fin.
Problème 1. Léa dessine des cercles dont le rayon mesure deux centimètres. Combien devra-t-elle dessiner de cercles pour avoir la même superficie qu’un cercle de 40 centimètres de diamètre ?

Problème 2. Daniel partage une pizza. Chaque pointe mesure 10 centimètres de côté et a un angle au centre de 45°. Quelle est l’aire de chaque pointe ?

Problème 3. Le diamètre d’une roue est 40 centimètres. Combien de tours complets aura fait la roue quand elle aura parcouru 50 mètres ?

Problème 4. Martine dessine un cercle dont le rayon mesure 15 centimètres. À l’intérieur, elle dessine deux cercles dont le rayon est de six centimètres. Quelle est la superficie de l’espace non couvert ?

Problème 5. Claude a deux rondelles dont les rayons mesurent respectivement cinq et neuf centimètres. Il dépose la plus petite sur la plus grande. Quelle est la superficie de l’espace non recouvert ?

Problème 6. Une mouche marche sur le contour d’une assiette dont le diamètre est de 20 centimètres. Elle parcourt un huitième du contour avant d’être chassée. Quelle est la longueur du parcours effectué par la mouche ?

Problème 7. Bernard note que le tour d’un arbre mesure 2,2 mètres. S’il devait transpercer l’arbre horizontalement d’un côté à l’autre en passant par le centre, quelle serait la longueur de l’aiguille intérieure ?

Problème 8. Michel découpe dans du carton un cercle dont le diamètre mesure 10 centimètres. Il trace deux rayons qui forment un angle de 30° et découpe cette partie Quelle est l'aire de la partie découpée ?

Solutions
Solution 1. L’aire d’un cercle dont le rayon mesure 2 cm est 4p cm². L’aire d’un cercle dont le diamètre mesure 40 cm est 400p cm². Léa doit dessiner 400p ÷ 4p = 100 cercles.

Solution 2. Comme l’angle au centre est de 45°, il y a 360 ÷ 45 = 8 pièces. L’aire de la pizza est 100p cm². L’aire de chaque pointe est 100p ÷ 8 = 39,3 cm².

Solution 3. La circonférence de la roue est 40p cm. Un parcours de 50 m correspond à un parcours de 5000 cm. La roue fait 5000 ÷ 40p = 39,8 tours. La roue aura fait 39 tours complets.

Solution 4. L’aire du grand cercle est 225p cm². L’aire d’un petit cercle est 36p cm². L’espace non couvert est 225p - (2 ´ 36p) = 480,7 cm².

Solution 5. L’aire de la grande rondelle est 81p cm². L’aire de l’autre est 25p cm². L’aire de l’espace non recouvert est 81p - 25p = 175,9 cm².

Solution 6. La circonférence de l’assiette est 20p cm. La mouche parcourt 20p ¸ 8 = 7,85 cm.

Solution 7. La circonférence est 2,2 mètres. On calcule le diamètre. On divise 2,2 par p : ce qui donne 0,7 m ou 70 cm.

Solution 8. L’angle étant de 30°, la partie est un douzième du cercle. L’aire du cercle est 25p cm². L’aire de la partie découpée est 25p ÷ 12 = 6,55 cm².

© Charles-É. Jean