Fraction

Une ou plusieurs parties d’un tout divisées en un nombre de parties de même grandeur ou de même mesure. On représente une fraction au moyen de deux nombres placés l’un au-dessous de l’autre et séparés par un trait. Toute fraction ainsi représentée est dite fraction ordinaire.

Numérateur
Le nombre supérieur s’appelle le numérateur. Par exemple, dans 4/7, le nombre 4 est le numérateur. Le numérateur correspond au nombre de parties retenues par rapport au nombre de parties qui constituent le tout. La fraction 4/7 désigne quatre parties sur sept parties.

Dénominateur
Le nombre inférieur est le dénominateur.  Par exemple, dans 4/7, le nombre 7 est le dénominateur. Le tout est composé de 7 parties.

Termes de la fraction

Le numérateur et le dénominateur sont les deux termes de la fraction.

Lecture de la fraction

Pour lire une fraction on exprime le numérateur puis le dénominateur qui se termine en ième. Par exemple, 4/7 se lit quatre septièmes. Il y a exception pour les dénominateurs 2, 3 ou 4 qui sont exprimés respectivement par demi, tiers ou quart.

Fraction unitaire

Toute fraction de la forme 1/n où n est un entier naturel non nul. Les 10 plus grandes fractions unitaires sont : 1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10. Les différences successives de deux fractions unitaires sont : 1/2, 1/6, 1/12, 1/20, 1/30, 1/42, 1/56, 1/72, 1/90. Le dénominateur est un nombre hétéromèque.

Fraction propre

Fraction dont le numérateur est plus petit que le dénominateur. Toute fraction propre est inférieure à 1. Exemple. 2/3.

Fraction impropre

Fraction dont le numérateur est plus grand que le dénominateur. Toute fraction impropre est supérieure à 1. Exemple. 5/2. Une fraction impropre est aussi dite expression fractionnaire.

Fraction réductible

Fraction dont le numérateur et le dénominateur ont au moins un diviseur entier commun. La fraction 12/36 a comme facteurs communs 2, 3, 4, 6 ou 12. Elle est égale à 6/18, 4/12, 3/9, 2/6, 1/3.

Fraction irréductible

Fraction dont le numérateur et le dénominateur n’ont pas de diviseur entier commun. On dit que le numérateur et le dénominateur sont premiers entre eux. Exemples. 2/3, 12/17, 3/20.

Fraction équivalente

Ensemble de fractions qui sont égales à une fraction irréductible. Par exemple, 1/3, 2/6, 3/9, 4/12, 5/15, ... sont des fractions équivalentes.

Fraction complexe

Fraction dont le numérateur et le dénominateur sont eux-mêmes des fractions, comme

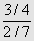 . Cette fraction est équivalente à 3/4 ÷ 2/7 = 3/4 × 7/2 = 21/8.

Fraction périodique

Fraction décimale dans laquelle il y a répétition d’un entier ou d’un groupe d’entiers. Par exemple, 1/3 donne la fraction périodique 0,3333 ..., 7/11 donne la fraction périodique 0,63 63 63 ... et 2/7 donne la fraction périodique 0,285714 285714 ... Chaque groupe de chiffres qui se reproduit est appelé période. Pour convertir une fraction périodique en fraction ordinaire, on prend le nombre correspondant à une période comme numérateur et on le divise par un nombre formé d’autant de 9 que de chiffres du numérateur. Par exemple, 0,285714 285714 ... est égal à 285 714/999 999.

Nombre fractionnaire

Nombre entier suivi d’une fraction. Un nombre fractionnaire est équivalent à une expression fractionnaire. Par exemple, 15/2 est une expression fractionnaire et 7 1/2 qui lui est équivalent est un nombre fractionnaire.

Pour cent

Fraction dont le dénominateur est 100. Ainsi, 15 pour cent signifie qu’il y a 15 unités sur 100 unités. On écrit en abrégé 15 %. Par exemple, Ginette a réussi dans trois travaux scolaires sur quatre, son taux de succès est de 75 %. Aussi, 75 % est équivalent à 75/100 ou 0,75.

Conversion d'une fraction

Une fraction ordinaire peut être convertie en une fraction décimale, en une fraction dont le dénominateur est une puissance de 10 ou en pourcentage. Voici un tableau qui donne la conversion de quelques fractions ordinaires dont le numérateur est 1 :

Opérations sur les fractions ordinaires

1. Pour additionner des fractions ordinaires, on les réduit au même dénominateur (normalement le plus petit) s’il y a lieu ; on transforme le numérateur par rapport au nouveau dénominateur puis on additionne les numérateurs. 

Soit à additionner 3/5, 2/3 et 7/20, le plus petit dénominateur commun est 5 × 3 × 4 = 60. La fraction 3/5 devient 36/60 ; 2/3 devient 40/60 et 7/20 devient 21/60. Le numérateur est 36 + 40 + 21 = 97. La somme est 97/60. Le dénominateur commun est aussi le plus petit commun multiple.

2. Pour soustraire deux fractions ordinaires, on les réduit au même dénominateur (normalement le plus petit) s’il y a lieu ; on transforme le numérateur par rapport au nouveau dénominateur puis on soustrait les numérateurs. 

Soit à calculer 4/5 - 8/11, le plus petit dénominateur commun est 5 × 11 = 55. La fraction 4/5 devient 44/55, 8/11 devient 40/55. Le numérateur est 44 - 40 = 4. La différence est 4/55.

3. Pour multiplier deux fractions ordinaires, on multiplie les numérateurs entre eux et les dénominateurs entre eux. Au besoin, on simplifie la fraction trouvée. 

Soit à multiplier 2/3, 4/7 et 11/12. On fait : 2 × 4 × 11 = 88, 3 × 7 × 12 = 252. La fraction est 88/252 qu’on peut réduire à 22/63. Avant d’effectuer la multiplication, on peut simplifier certains termes du numérateur avec ceux du dénominateur.

4. Pour diviser deux fractions ordinaires, on multiplie la première fraction par la seconde renversée. Au besoin, on simplifie la fraction trouvée. 

Soit à diviser 2/3 par 8/9, on fait 2/3 × 9/8 = 18/24. On peut réduire cette fraction à 3/4.

Sens de la fraction

Une fraction peut aussi avoir les sens suivants :
1. Une fraction est un rapport. Un rapport sert à comparer des quantités d'éléments ou des grandeurs de même unité. Exemple. Sur 25 heures de cours, j'ai huit heures de mathématiques. Le rapport est 8/25.

2. Une fraction est un taux. Un taux sert à comparer des quantités d'éléments ou des grandeurs d'unité différente. Exemple. J'ai mangé trois pommes en quatre jours. Le taux est de 3/4 pomme par jour.

3. Une fraction exprime une probabilité. Exemple. J'ai trois chances sur quatre de gagner un prix. Ma chance est de 3/4.

On peut écrire le nombre 9 sous formes de fractions ordinaires en utilisant des chiffres différents. Dans les trois premiers exemples, on utilise les chiffres de 1 à 9 et dans les trois autres les chiffres de 0 à 9.

On peut construire des carrés magiques avec des fractions. En voici un dont la densité est 17/10 ou 1,7 :

© Charles-É. Jean