|
Hétéromèque
°
Nombre hétéromèque.
– Nombre rectangulaire
dont un côté du rectangle mesure une unité de plus que l'autre. Le terme
général de rang n est n(n + 1). Les six plus petits
hétéromèques peuvent être représentés ainsi :
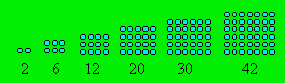
Lorsqu’on fait le produit de deux entiers dont la
différence est 1, le plus petit entier est le rang de l’hétéromèque. Pour
trouver son successeur, on lui additionne deux fois le rang suivant. Par
exemple, 182 est un hétéromèque car 182 = 13 × 14. Il est de rang 13.
Son successeur est 182 + 2 × 14 = 210.
Voici les 49 plus petits
hétéromèques :
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
2 |
6 |
12 |
20 |
30 |
42 |
56 |
72 |
90 |
|
1 |
110 |
132 |
156 |
182 |
210 |
240 |
272 |
306 |
342 |
380 |
|
2 |
420 |
462 |
506 |
552 |
600 |
650 |
702 |
756 |
812 |
870 |
|
3 |
930 |
992 |
1056 |
1122 |
1190 |
1260 |
1332 |
1406 |
1482 |
1560 |
|
4 |
1640 |
1722 |
1806 |
1892 |
1980 |
2070 |
2162 |
2256 |
2352 |
2450 |
Voici quelques
propriétés concernant les nombres de cette classe :
La période des unités des nombres successifs correspond à un nombre de cinq chiffres :
26 200.
Les unités sont 0, 2 et 6.
La somme des n premiers hétéromèques est le double d’un tétraédrique.
Tous les hétéromèques sont pairs, car ils sont le produit d’un impair et d’un
pair.
Tout hétéromèque de rang n est la somme de pairs successifs de 2
jusqu'à 2n.
La différence de deux hétéromèques successifs est égale au double du rang
du plus grand.
Un hétéromèque de rang n est égal au double du triangulaire
de même rang.
Un hétéromèque de rang n est la somme de n et de son carré.
La somme du carré de n et d'un hétéromèque de rang n est un
triangulaire de rang 2n.
La somme d’un hétéromèque de rang n et du carré précédent est un
triangulaire de rang 2n.
La somme d’un hétéromèque de rang n et du carré suivant est un
triangulaire de rang (2n + 1).
La somme d’un hétéromèque de rang n et d’un autre de rang (n
+ 1) est égale au double du carré de rang (n + 1).
La somme d’un hétéromèque de rang n, d’un autre de rang (n
+ 1) et de deux fois le carré situé entre eux est un carré de rang (2n
+ 2).
La somme d’un carré de rang n, d’un autre de rang (n + 1) et
du carré de l’hétéromèque situé entre eux est un carré de rang (n2
+ n + 1).
Les nombres suivants sont à la fois
palindromes et hétéromèques.
|
2 |
6 |
272 |
6 006 |
289 982 |
|
2 629 262 |
6 039 306 |
27 999 972 |
28 233 282 |
2 704 884 072 |
Un hétéromèque étant donné, pour connaître les mesures du
rectangle qui l’a généré, on procède ainsi : On extrait la racine
carrée de ce nombre. On retient la partie entière et l’entier suivant. Soit
l'hétéromèque 1332, sa racine carrée est 36,496 ... On retient 36 ; le
suivant est 37. D’où, 1332 = 36 × 37.
Tout rectangulaire non carré ou non
hétéromèque est dit promèque. Les
hétéromèques sont des nombres figurés.
© Charles-É. Jean
Index
: H
|
![]()
![]()