Récréomath Défis 95

Série A 95. Évasions routières Depuis plusieurs semaines, Roméo et Lyne préparent leur voyage de l’été. Leur départ se fait au même endroit, mais pas le même jour. Chacun emprunte exactement le même itinéraire. Roméo part le 9 juillet. Il roule pendant 133 kilomètres le premier jour. Par la suite, il augmente sa course de six kilomètres par jour. Lyne quitte le 14 juillet. Elle parcourt 345 kilomètres ce jour-là. Puis, elle diminue sa course de sept kilomètres par jour. En quel jour Roméo et Lyne vont-ils parcourir la même distance ? Solution	L’algorithme de Liouville est un algorithme qui permet d'établir des identités dans lesquelles la somme des cubes de certains entiers est égale au carré de leur somme.
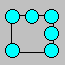
Série B 95. Monnaie d’Alexia Alexia dépose six pièces de monnaie, comme il est illustré. Elle dit à Alexis : - J’ai formé deux rangées de deux pièces et deux rangées de trois pièces. Tu dois placer deux autres pièces et réussir sept rangées de trois pièces. Où Alexis devra-t-il placer les deux pièces additionnelles ? Solution	Combien peut-on obtenir de combinaisons de trois nombres différents dont la somme est 11 avec les nombres de 1 à 7 ? Solution
Série C 95. Noisettes de Mathieu Mathieu a un sac de noisettes. Il veut partager ses noisettes en parts égales entre un certain nombre d’enfants. Toutefois, il ne veut pas donner toutes les noisettes à un seul enfant ni donner une noisette par enfant. Par exemple, s’il a 32 noisettes, il pourra donner 2 noisettes à 16 enfants, 4 noisettes à 8 enfants, 8 noisettes à 4 enfants ou 16 noisettes à 2 enfants. Il y quatre possibilités de partage. Trouvez un algorithme qui permet de déterminer le nombre de possibilités de partage lorsque le sac contient un nombre de noisettes donné. Solution © Charles-É. Jean	Le calendrier de Lucas est un ensemble de tableaux qui permettent de trouver le jour de la semaine d'une date donnée dans le calendrier grégorien.