|
Série
A
Solution 95
Le 14
juillet Roméo a parcouru 163 kilomètres et Lyne 345 kilomètres. Les deux se
rapprochent de 13 kilomètres chaque jour. On fait
: (345 - 163) ¸
13 = 14 jours.
Chacun des deux va
parcourir 247 kilomètres le 28 juillet.
Retour
au problème
|
L’algorithme
de Liouville
est un algorithme qui permet d'établir des identités dans lesquelles
la somme des cubes de certains entiers est égale au carré de leur
somme.
|
|
Série B
Solution 95
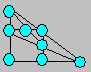
Il
faut que chacune des pièces posées soit à l’intersection de deux ou de
trois rangées. En plaçant, dans des positions appropriées, un jeton à l’extrémité
de la rangée inférieure et un autre à l’extrémité de la première rangée
verticale, on peut réussir l’atteinte de sept rangées. Voici un
exemple :
Retour
au problème
|
Solution de l’énigme
Quatre combinaisons : (1, 3, 7), (1, 4, 6), (2, 3, 6), (2, 4, 5)
|
|
Série C
Solution 95
Un
nombre de noisettes étant donné,
100. On extrait
la racine carrée qui est exprimée en notation décimale.
110. On trouve
les facteurs du nombre donné en excluant 1 et ceux supérieurs au
résultat de la ligne 100.
120. On compte
le nombre de facteurs.
130. On
multiplie par 2.
140. Si le résultat de la ligne
100 est un entier, on soustrait 1. Û
Le résultat est le nombre de possibilités de partage.
Soit 66 le nombre de noisettes. La racine carrée de 66
est 8,12. En excluant 1, les facteurs de 66 inférieurs à la racine
carrée sont 2, 3 et 6. On compte trois facteurs. En multipliant par 2, on
obtient 6. Il y a six possibilités de partage. En effet, Mathieu pourra
donner 2 noisettes à 33 enfants, 3 noisettes à 22 enfants, 6 noisettes
à 11 enfants, 11 noisettes à 6 enfants, 22 noisettes à 3 enfants ou 33
noisettes à 2 enfants.
Retour
au problème
|
Le calendrier de
Lucas est un ensemble de
tableaux qui permettent de trouver le jour de la semaine d'une date
donnée dans le calendrier grégorien.
|
![]()
![]()