|
k |
k +
3x
+ 2y |
k +
3y |
k +
3x
+ y |
|
k + x +
3y |
k +
2x
+ y |
k + x |
k +
2x
+ 2y |
|
k +
3x |
k +
2y |
k +
3x
+ 3y |
k + y |
|
k +
2x
+ 3y |
k + x+ y |
k +
2x |
k + x+
2y |
Chacun des carrés engendre une infinité de carrés magiques. Dans le premier
cas, si k = 5, x = 3 et y = 1, on obtient un carré magique
normal. Dans le second cas, si k = 1, x = 1 et y = 4, on
obtient également un carré magique normal qui, en plus, est diabolique.
En dehors des carrés magiques, il
existe d’autres formes de treillis magiques généraux. On en donne deux
exemples.
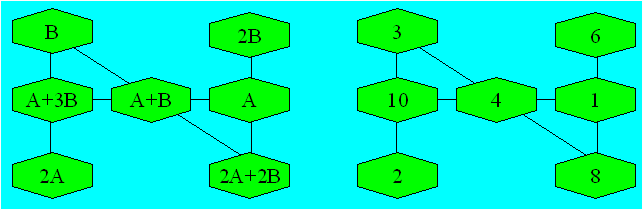
1e La figure de gauche
est un treillis magique général dont la somme des expressions algébriques
dans chaque rangée reliée par une droite est (3A + 4B). On peut donner
toute valeur arbitraire aux variables A et B. Si on pose A = 1 et B = 3, on
a le treillis de droite dont la somme par rangée est 15.
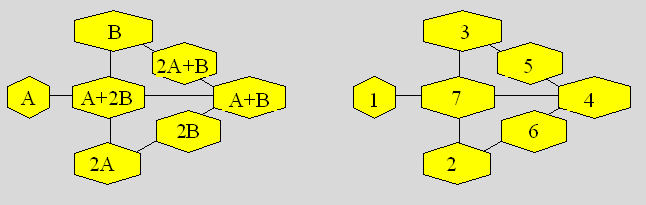
2e Dans la figure de
gauche ci-après, la somme des expressions dans chaque rangée est (3A +
3B). Si on pose A = 1 et B = 3, on obtient le treillis de droite dont la
somme par rangée est 12.
Il
existe un grand nombre de treillis magiques généraux.
© Charles-É. Jean
![]()
![]()